ФИЗИКО-МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СЛОЖНЫХ ЭЛЕМЕНТОВ АКРОБАТИЧЕСКОГО РОК-Н-РОЛЛА
Адашевский В.М.1, Ермаков С.С. 2, Фирсова Ю.Ю.1
Национальный технический университет "ХПИ" 1
Харьковская государственная академия физической культуры2
Аннотация. Показаны направления биомеханического обоснования выполнения элемента акробатического рок-н-ролла Фус-сальто с учётом конкретных физических данных спортсменов. Разработана математическая модель для определения влияния на качество выполнения технического элемента таких параметров как: скорость и угол вылета центра масс тела спортсмена, положение центра масс тела спортсмена в начальных фазах бросковых упражнений, начальная угловая скорость вращения тела спортсмена. Определены параметры влияния осевых моментов инерции при различных группировках тела на угловую скорость вращения тела спортсмена в полете и сил сопротивления воздушной среды на характеристики полёта тела. Показаны направления выбора необходимых биомеханических характеристик, которые способны реализовать спортсмены. Предложены рекомендации по повышению эффективности выполнения элемента акробатического рок-н-ролла Фус-сальто.
Ключевые слова: рок-н-ролл, биомеханический, траектория, бросок.
Анотацiя. Адашевський В.М., Ермаков С.С., Фирсова Ю.Ю. Фiзико-математичне моделювання складних елементiв акробатичного рок-н-ролу. Показанi напрями бiомеханiчного обгрунтування виконання елементу акробатичного рок-н-ролу Фус-сальто з врахуванням конкретних фiзичних даних спортсменiв. Розроблена математична модель для визначення впливу на якiсть виконання технiчного елементу таких параметрiв як: швидкiсть i кут вильоту центру мас тiла спортсмена, положення центру мас тiла спортсмена в початкових фазах кидкових вправ, початкова кутова швидкiсть обертання тiла спортсмена. Визначенi параметри впливу осьових моментiв iнерцii при рiзних угрупуваннях тiла на кутову швидкiсть обертання тiла спортсмена у польотi i сил опору повiтряноi середи на характеристики польоту тiла. Показанi напрями вибору необхiдних бiомеханiчних характеристик, якi здатнi реалiзувати спортсмени. Запропонованi рекомендацii по пiдвищенню ефективностi виконання елементу акробатичного рок-н-ролу Фус-сальто.
Ключовi слова: рок-н-рол, бiомеханiчний, траекторiя, кидок.
Annotation. Adashevskiy V.M., Iermakov S.S., Firsova Iu.Iu. Physical mathematical modelling of difficult elements of acrobatic rock-and-roll. It is shown directions of biomechanics substantiation of implementation acrobatic rock-and-roll Fus-salto element taking into account concrete physical data of sportsmen. Mathematical model is developed for determination the influence on a quality of implementation of technical element of such parameters as: speed and angle of flight of centre-of-mass sportsman’s body, position of centre-of-mass body of sportsman in the initial phases of throw exercises, initial angular velocity of rotation of body of sportsman. It is developed mathematical model to determine the impact on the quality of the technical element parameters such as speed and angle of flight of centre-of-mass of the athlete's body, the position of center-of-mass of the athlete's body in the initial phases of throwing exercises in the initial angular velocity of the athlete's body. The parameters of exposure axial moments of inertia for different groupings of body angular velocity the athlete's body in flight and air resistance forces of environment to flight characteristics of the body. Directions of choice of necessary biomechanics descriptions which are able to realize sportsmen are shown. It is offered recommendations are on the increase of efficiency of implementation of element of acrobatic rock-and-roll of Fus-salto.
Keywords: rock-and-roll, biomechanics, trajectory, throw.
Введение.
Акробатический рок-н-ролл относится к группе сложно координационных видов спорта, содержание технических элементов в котором основано на взаимодействии партнеров и представленное в виде двигательной композиции с музыкальным сопровождением. В основе акробатических элементов рок-н-ролла лежат такие движения как: броски, полеты и ловля партнера, взаимные перемещения, позы с удержанием равновесия в статике и динамике и другие. Одним из наиболее сложных элементов является "Фус - сальто" - безопорное вращение тела партнёрши с полным переворачиванием через голову, выполняемое за счет взброса партнером толчком в ступню ноги партнерши, которую она ставит на его соединенные кисти рук [10, 11, 15]. В этом случае наиболее целесообразным представляется использование методов математического моделирования, с целью получения оптимальных биомеханических параметров движений партнеров.
Спортивный результат в сложном элементе акробатического рок-н-ролла "Фус - сальто" определяется в основном рациональными биомеханическими характеристиками, которые способен реализовать спортсмен и которые зависят от:
- скорости вылета и угла вылета центра масс тела спортсмена,
- положения центра масс тела спортсмена в начальных фазах бросковых упражнений,
- начальной угловой скорости вращения тела спортсмена,
- влияния осевых моментов инерции при различных группировках тела на угловую скорость вращения тела спортсмена в полете,
- влияния сил сопротивления воздушной среды на характеристики полёта тела.
Эти биомеханические характеристики при рациональных их значениях и сочетаниях с учётом конкретных физических данных спортсмена позволят на высоком техническом уровне выполнить "Фус - сальто" , а спортсмен соответственно получить высокую оценку.
Теоретической основой исследований о биомеханических закономерностях спортивных движений являются работы Н.А. Бернштейна [2], В.М. Зациорского [7], А.Н. Лапутина [4, 8].
Необходимость предварительного построения моделей и последующего выбора наиболее рациональных биомеханических параметров движений спортсмена отмечается в работах Адашевского В.М. [1, 2, 14 ], Ермакова С.С. [6, 14], Lin C-F. [12], Pengelly F. [13] и других.
Важное значение при этом приобретает поиск оптимального сочетания кинематических и динамических параметров движений спортсмена [9, 12-14] с учетом закономерной передачи механической энергии от звена к звену [4, 5, 8]. Такой подход позволяет успешно влиять на результат спортивной деятельности [4, 8]. При этом рекомендуется использовать математические модели движений [1, 6, 12-14].
Поэтому очевидна необходимость проведения более детальных теоретических и практических исследований с использованием методов математического моделирования.
Исследования проводились по госбюджетной теме М0501. "Разработка инновационных методов и методов диагностики ведущих видов подготовленности спортсменов разной квалификации и специализации" 2012-2013г.г.
Цель, задачи работы, материал и методы.
Цель работы - заключалась в определении основных рациональных биомеханических характеристик в сложном элементе акробатического рок-н-ролла "Фус - сальто" с учётом конкретных физических данных спортсменов, а также в составлении рекомендаций, которые повышают технику, а, соответственно, судейскую оценку.
Задачи работы:
- выполнить критический анализ специальной литературы,
- составить расчётную схему для определения основных рациональных биомеханических характеристик: скорости вылета и угла вылета центра масс тела спортсмена, положения центра масс тела спортсмена в начальных фазах бросковых упражнений, начальной угловой скорости вращения тела спортсмена, влияние осевых моментов инерции при различных группировках тела на угловую скорость вращения тела спортсмена в полете, влияние сил сопротивления воздушной среды на характеристики полета в элементе акробатического рок-н-ролла "Фус - сальто" .
- составить физико-математическую модель для определения основных рациональных биомеханических характеристик полета в элементе акробатического рок-н-ролла "Фус - сальто" ,
- определить основные биомеханические характеристики полёта тела путём решения задачи динамики биомеханической системы,
- провести исследование биомеханических характеристик и получить их графические зависимости,
- составить рекомендации относительно улучшения оценок в "Фус - сальто" .
В решении задач использовался специальный программный комплекс "КИДИМ" , разработанный на кафедре теоретической механики НТУ "ХПИ" .
Результаты исследования.
Рассмотрим расчётные схемы для определения основных рациональных биомеханических характеристик в элементе акробатического рок-н-ролла "Фус - сальто" с учётом конкретных физических данных спортсмена (рис. 1, 2).
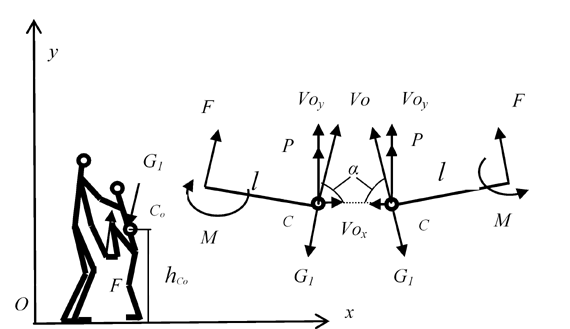
Рис. 1. Расчётная схема для определения начальных рациональных биомеханических характеристик броска
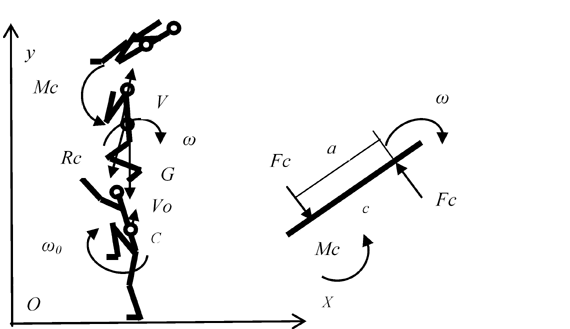
Рис. 2. Расчётная схема для определения рациональных биомеханических характеристик в фазе полёта
V0 - начальная скорость вылета центра масс тела спортсмена,
VоX - проекция скорости вылета центра масс на осьOx ,
VоY - проекция скорости вылета центра масс на ось Oy,
В проекциях на оси декартовой абсолютной системы координат:
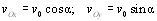
Выражение абсолютной начальной скорости вылета
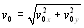
hC0 - высота центра масс тела в начальное время вылета,
α0=α - σгол вылета центра масс спортсмена во время броска,
G - сила тяжести,
hC - текущая высота центра масс тела,
Rc - сила сопротивления воздушной среды,
Mc - момент сил сопротивления воздушной среды воздушной среды,
где Mc = (Fc)a,
Для решения
поставленной задачи сила аэродинамического сопротивления Rc для тел,
движущихся в воздушной среде плотностью r , равна 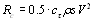 ;
; 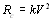 .
Fc - равнодействующая распределённых сил сопротивления воздушной среды
.
Fc - равнодействующая распределённых сил сопротивления воздушной среды
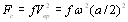 или
или 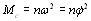 .
.
При подсчёте
этих сил безразмерные коэффициенты лобового сопротивления
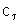 определяют экспериментально в зависимости от
формы тела и его ориентации в среде. Величина S (мидель) определяется значением
проекции площади поперечного сечения тела на плоскость перпендикулярную оси
движения, V - абсолютная скорость тела. Известно, что плотность воздуха -
r = 1,3 кг/м3. Необходимо отметить, что тело, в
полете совершает плоскопараллельное движение. Угол поворота тела в сагиттальной
анатомической плоскости соответственно изменяется величина S. Определение
переменных значений миделя S и коэффициента лобового сопротивления
определяют экспериментально в зависимости от
формы тела и его ориентации в среде. Величина S (мидель) определяется значением
проекции площади поперечного сечения тела на плоскость перпендикулярную оси
движения, V - абсолютная скорость тела. Известно, что плотность воздуха -
r = 1,3 кг/м3. Необходимо отметить, что тело, в
полете совершает плоскопараллельное движение. Угол поворота тела в сагиттальной
анатомической плоскости соответственно изменяется величина S. Определение
переменных значений миделя S и коэффициента лобового сопротивления
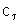 требуют основательных дополнительных
исследований, поэтому при решении данной задачи примем их усреднённые значения в
допустимых границах.
требуют основательных дополнительных
исследований, поэтому при решении данной задачи примем их усреднённые значения в
допустимых границах.
Тогда значения коэффициентов k и f:
k = 0 - 2кг/м; n =0 - 0.04 кг/м2.
Так как тело спортсмена в фазе полёта движется в одной из анатомических плоскостей - сагиттальной плоскости, составим уравнения динамики плоскопараллельного движения в проекциях на оси координат.
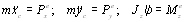 .
.
Здесь m - масса
тела,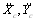 - соответствуют проекциям ускорения центра
масс,
- соответствуют проекциям ускорения центра
масс,
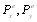 - проекции равнодействующей внешних сил
действующих на тело,
- проекции равнодействующей внешних сил
действующих на тело, ![]() - момент
инерции относительно фронтальной оси.
- момент
инерции относительно фронтальной оси.
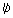 - соответствует угловому ускорению при повороте
тела вокруг фронтальной оси,
- соответствует угловому ускорению при повороте
тела вокруг фронтальной оси,
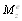 - суммарный момент внешних сил сопротивления
среды относительно фронтальной оси.
- суммарный момент внешних сил сопротивления
среды относительно фронтальной оси.
При движении в плоскости xAy, систему уравнений можно записать так:
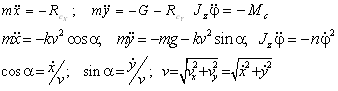
α - σгол между текущими проекциями скорости центра масс тела и вектором его скорости.
Решение этой задачи требует интегрирования дифференциальных уравнений движения.
Такая операция легко выполняется с помощью специального программного комплекса "КИДИМ" , разработанного на кафедре теоретической механики НТУ "ХПИ" .
Определим зависимость основных рациональных биомеханических характеристик в элементе акробатического рок-н-ролла "Фус - сальто" с учётом конкретных физических данных спортсмена от: скорости вылета и угла вылета центра масс тела спортсмена, положения центра масс тела спортсмена в начальных фазах бросковых упражнений, начальной угловой скорости вращения тела спортсмена, значений осевых моментов инерции при различных группировках тела, значений сил сопротивления воздуха (рис. 3-9).
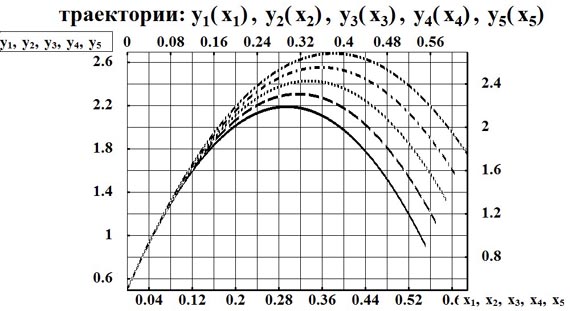
V0 =6.6 м/c; V0 =6.4м/c; V0 =6.2м/c; V0 =6.0 м/c; V0 =5.8 м/c.
Рис.3. Графические характеристики траектории центра масс для различных значений начальной скорости вылета
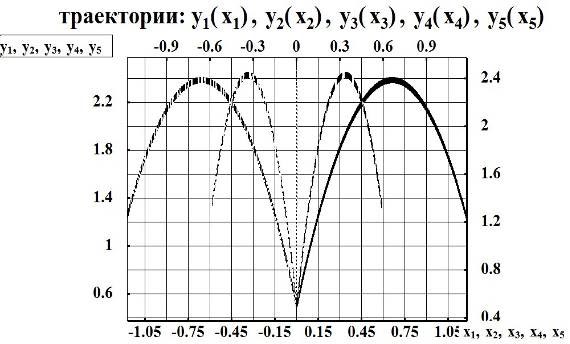
α0 =1000; α0 = 950; α0 =900; α0 =850; α0 =800.
Рис. 4. Графические характеристики зависимости траектории центра масс для различных значений углов вылета тела
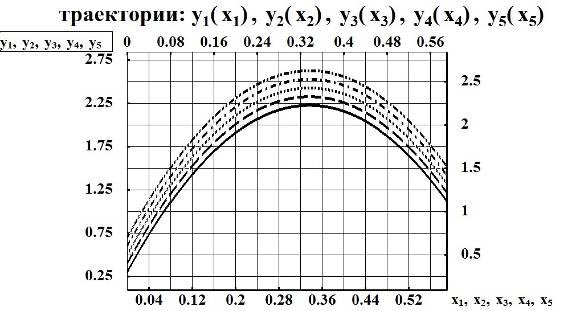
hC0=0.7м; hC0=0.6м; hC0=0.5м; hC0=0.4м; hC0=0.3м;
Рис. 5. Графические характеристики траектории центра масс для различных значений высоты центра масс тела во время броска
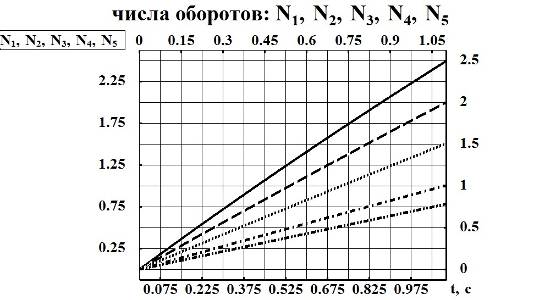
IC=6кгм2 ; IC=5кгм2; IC=4кгм2; IC=3кгм2; IC=2кгм2.
Рис. 6. Графические характеристики чисел оборотов для различных значений момента инерции относительно фронтальной оси
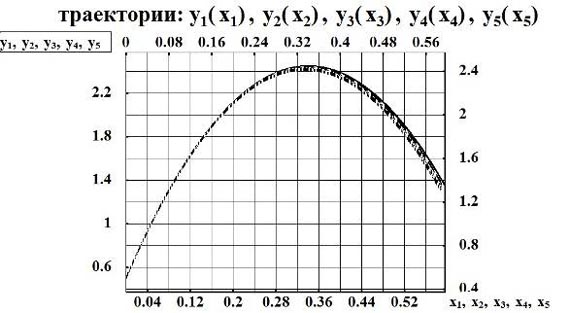
k =0.3 кг/м; k=0.25 кг/м; k =0.2 кг/м; k =0.1 кг/м; k =0 кг/м.
Рис.7. Графические характеристики траектории центра масс для различных значений коэффициентов сопротивления воздушной среды
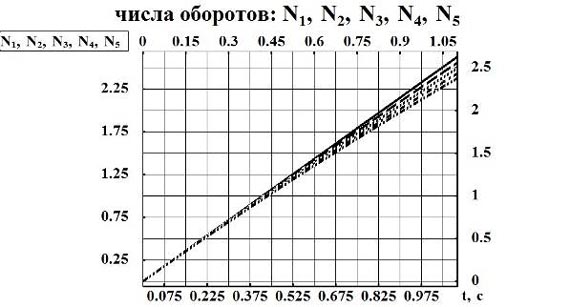
n=0.04кгм2; n=0.03кгм2; n=0.02кгм2; n=0.01кгм2; n=0кгм2.
Рис.8. Графические характеристики значений чисел оборотов для различных коэффициентов сопротивления воздушной среды
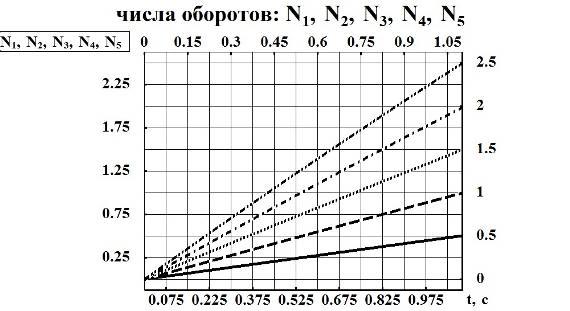
ω0=15.1рад/c; ω0=11.8 рад/c; ω0=8.8 рад/c; ω0=5.8 рад/c; ω0=2.9 рад/c.
Рис.9. Графические характеристики чисел оборотов для различных значений начальных угловых скоростей тела
Результаты расчётов математических моделей и полученные графические характеристики показывают:
- начальная скорость вылета и угол вылета центра масс тела, положение центра масс тела спортсмена в начальных фазах, тела спортсмена оказывают значительное влияние на характеристики полета (рис.3, 4),
- траектории центра масс для различных значений высоты центра масс тела во время броска изменяются в среднем на такие же значения (рис. 5),
- различные значения моментов инерции тела относительно фронтальной оси во время полёта существенно изменяют угловую скорость вращения тела, а, следовательно, и изменяют значения чисел оборотов N, что при рациональных позах может способствовать более быстрым вращениям вокруг фронтальной оси (рис. 6) и даже изменять значения чисел оборотов N в три раза,
- для реальных скоростей полёта тела спортсмена, сила сопротивления среды оказывает малое влияние на характеристики полета (рис. 7-8),
- значения чисел оборотов естественно прямо пропорциональны значениям начальных угловых скоростей тела (рис. 9).
Выводы
Анализ полученных в результате расчётов графических характеристик показывает, что для достижения высоких результатов необходимо увеличивать начальную скорость вылета, высоту центра масс тела во время вылета, уменьшать моменты инерции, что позволит увеличить угловую скорость вращения в группировках, уменьшать углы вылета центра масс тела, при рациональном сочетании перечисленных параметров.
Таким образом, построенные графические характеристики позволяют при их анализе и последующем их использовании улучшить результат с учётом конкретных физических данных и возможностей спортсменов.
Литература
1. Адашевский В.М. Теоретические основы механики биосистем. - Харьков: НТУ "ХПИ" , 2001. - 260 с.
2. Адашевський В.М. Метрологiя у спортi. - Харкiв: НТУ "ХПI" , 2010. - 76 с.
3. Бернштейн Н.А. Очерки по физиологии движений и физиологии активности. - М.: Медицина, 1966. -349 с.
4. Бiомеханiка спорту / За ред. А.М. Лапутiна. - К.: Олiмпiйська лiтература, 2001. - 320 с.
5. Бусленко Н.П. Моделирование сложных систем. - М.: Наука, 1988. - 400 с.
6. Ермаков С.С. Обучение технике ударных движений в спортивных играх на основе их компьютерных моделей и новых тренажерных устройств: автореф. дис. ... д-ра пед. наук: 24.00.01. - Киев, 1997. - 47 с.
7. Зациорский В.М., Аурин А.С., Селуянов В.Н. Биомеханика двигательного аппарата человека. - М.: ФиC, 1981. - 143 с.
8. Лапутин А.Н. Обучение спортивным движениям. - К.: Здоров'я, 1986. - 216 с.
9. Adouni M., Shirazi-Adl A. Knee joint biomechanics in closed-kinetic-chain exercises. Computer Methods in Biomechanics and Biomedical Engineering. 2009, vol.12(6), pp. 661- 670. doi:10.1080/10255840902828375.
10. Frömel K., Stratton G., Vasendova J., Pangrazi R.P. Dance as a Fitness Activity the Impact of Teaching Style and Dance Form. Journal of Physical Education, Recreation & Dance. 2002, vol.73(5), pp. 26- 30. doi:10.1080/07303084.2002.10607805.
11. Li F-X., Margetts S., Fowler I. Use of "chalk" in rock climbing: sine qua non or myth? Journal of Sports Sciences. 2001, vol.19(6), pp. 427- 432. doi:10.1080/026404101300149375.
12. Lin C-F., Su F-C., Wu H-W. Ankle biomechanics of ballet Dancers in relevé en pointé dance. Research in Sports Medicine. 2005, vol.13(1), pp. 23- 35. doi:10.1080/15438620590922068.
13. Pengelly F. Anatomy for Dance: An Expanded Design. Journal of Dance Education. 2010, vol.10(3), pp. 77- 82. doi:10.1080/15290824.2010.508696.
14. Volodymyr Adashevsky, Sergii Iermakov, Krzystof Prusik, Katarzyna Prusik, Karol Gorner. Biomechanics: theory and practice. Gdansk, Zdrowie-Projekt, 2012, 184 p.
15. Waite L. Rock and Roll! Using Classic Rock as a Guide to Fantasy-Theme Analysis. Communication Teacher. 2008, vol.22(1), pp. 10- 13. doi:10.1080/17404620801914491.
References:
1. Adashevskij V.M. Teoreticheskie osnovy mekhaniki biosistem [Theoretical basis of mechanics of biosystems], Kharkov, KPI Publ., 2001, 260 p.
2. Adashevs'kij V.M. Metrologiia u sporti [Metrology in sport], Kharkov, KPI Publ., 2010, 76 p.
3. Bernshtejn N.A. Ocherki po fiziologii dvizhenij i fiziologii aktivnosti [Essays on physiology of motions and physiology of activity], Moscow, Medicine, 1966, 349 p.
4. Laputin A.M. Biomekhanika sportu [Biomechanics of sport], Kiev, Olympic literature, 2001, 320 p.
5. Buslenko N.P. Modelirovanie slozhnykh sistem [Modeling of complex systems], Moscow, Science, 1988, 400 p.
6. Iermakov S.S. Obuchenie tekhnike udarnykh dvizhenij v sportivnykh igrakh na osnove ikh komp'iuternykh modelej i novykh trenazhernykh ustrojstv [Education to the technique of shock motions in sport games on the basis of their computer models and new trainer devices], Dokt. Diss., Kiev, 1997, 47 p.
7. Zaciorskij V.M., Aurin A.S., Seluianov V.N. Biomekhanika dvigatel'nogo apparata cheloveka [Biomechanics of motive vehicle of a man], Moscow, Physical Culture and Sport, 1981, 143 p.
8. Laputin A.N. Obuchenie sportivnym dvizheniiam [Education to sport motions], Kiev, Health, 1986, 216 p.
9. Adouni M., Shirazi-Adl A. Knee joint biomechanics in closed-kinetic-chain exercises. Computer Methods in Biomechanics and Biomedical Engineering. 2009, vol.12(6), pp. 661-670. doi:10.1080/10255840902828375.
10. Frömel K., Stratton G., Vasendova J., Pangrazi R.P. Dance as a Fitness Activity the Impact of Teaching Style and Dance Form. Journal of Physical Education, Recreation & Dance. 2002, vol.73(5), pp. 26- 30. doi:10.1080/07303084.2002.10607805.
11. Li F-X., Margetts S., Fowler I. Use of "chalk" in rock climbing: sine qua non or myth? Journal of Sports Sciences. 2001, vol.19(6), pp. 427- 432. doi:10.1080/026404101300149375.
12. Lin C-F., Su F-C., Wu H-W. Ankle biomechanics of ballet Dancers in relevé en pointé dance. Research in Sports Medicine. 2005, vol.13(1), pp. 23- 35. doi:10.1080/15438620590922068.
13. Pengelly F. Anatomy for Dance: An Expanded Design. Journal of Dance Education. 2010, vol.10(3), pp. 77- 82. doi:10.1080/15290824.2010.508696.
14. Volodymyr Adashevsky, Sergii Iermakov, Krzystof Prusik, Katarzyna Prusik, Karol Gorner. Biomechanics: theory and practice. Gdansk, Zdrowie-Projekt, 2012, 184 p.
15. Waite L. Rock and Roll! Using Classic Rock as a Guide to Fantasy-Theme Analysis. Communication Teacher. 2008, vol.22(1), pp. 10- 13. doi:10.1080/17404620801914491.
Информация об авторах:
Адашевский Владимир Михайлович
adashevsky@ukr.net
Национальный технический университет "ХПИ"
ул. Фрунзе 21, г. Харьков, 61002, Украина.
Ермаков Сергей Сидорович
sportart@gmail.com
Харьковская государственная академия физической культуры
ул. Клочковская 99, г. Харьков, 61022, Украина.
Фирсова Юлия Юрьевна
adashevsky@ukr.net
Национальный технический университет "ХПИ"
ул. Фрунзе 21, г. Харьков, 61002, Украина.
Поступила в редакцию 25.03.2013г.
Information about the authors:
Adashevskiy V.M.
adashevsky@ukr.net
National Technical University "KPI"
Frunze str. 21, Kharkov, 61002, Ukraine.
Iermakov S.S.
sportart@gmail.com
Kharkov State Academy of Physical Culture
Klochkovskaya str. 99, Kharkov, 61022, Ukraine.
Firsova Iu.Iu.
adashevsky@ukr.net
National Technical University "KPI"
Frunze str. 21, Kharkov, 61002, Ukraine.
Came to edition 25.03.2013.
http://dx.doi.org/10.6084/m9.figshare.662463