ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ И П РОБЛЕМА ИЗМЕРИМОСТИ В СПОРТИВНОЙ ПЕДАГОГИКЕ И СОРЕВНОВАНИЯХ
Сапцин В.М., Циповяз А.Т.
Кременчугский государственный университет имени Михаила Остроградского
Аннотация. Рассматривается проблема объективной оценки спортивных результатов и педагогического тестирования, которые всегда имеют случайную составляющую и зависят от внешних, внутренних, объективных и субъективных факторов. Дается анализ неопределенности с учетом новых концепций и математических подходов, основанных на физических и квантово-механических аналогиях. Предлагаются новые подходы к организации спортивных соревнований и ранжирования их участников.
Ключевые слова: спортивный результат, неопределенность, случайная составляющая, объективные, субъективные факторы, математические подходы, квантовая эконофизика.
Анотацiя. Сапцин В.М., Цiпов’яз А.Т. Принцип невизначеностi i проблема вимiрностi у спортивнiй педагогiцi й змаганнях. Розглядаеться проблема об’ективноi оцiнки спортивних результатiв i педагогiчного тестування, якi завжди мають випадкову складову i залежать вiд зовнiшнiх, внутрiшнiх, об’ективних i суб’ективних факторiв. Даеться аналiз невизначеностей з урахуванням нових концепцiй i математичних пiдходiв, що ґрунтуються на фiзичних i квантово-механiчних аналогiях. Пропонуються новi пiдходи до органiзацii спортивних змагань i ранжування iх учасникiв.
Ключовi слова: спортивний результат, невизначенiсть, випадкова складова, об’ективнi, суб’ективнi фактори, математичнi пiдходи, квантова еконофiзика.
Annotation. Saptsin V.M., Tsipoviaz A.T. The principle of uncertainty and the problem of measurability in sports pedagogy and competitions. The problem of objective estimation of sporting results and pedagogical testing is examined. They always have a casual constituent. They depend on external, internal, objective and subjective factors. An analysis over of vagueness is brought taking into account new conceptions and mathematical approaches. They are based on physical and quantum mechanical analogies. The new going is offered near organization of sporting competitions and ranging of their participants.
Keywords: athletic result, uncertainty, casual component, objective, subjective factors, mathematical approaches, quantizing econophysics.
Введение.
Проведение спортивных соревнований ставит своей целью выявление сильнейшего, призеров и ранжирование (установление относительных рейтингов) всех участников соревнования. Соревнования, согласно существующих классификаций [1, 2, 3 и др.], отличаются по видам спорта, массовости, характеру организации, рангу, способам оценки результата и т. п.
Одна из проблем как в спортивной педагогике, так и в спортивных состязаниях - это проблема измеримости, т. е. по возможности объективная оценка спортивных показателей участников соревнований, которая всегда имеет случайную составляющую и зависит от ряда других факторов: внешних, внутренних, объективных и субъективных.
Работа выполнена в соответствии с НИР Кременчугского государственного университета имени Михаила Остроградского.
Цель, задачи работы, материал и методы.
Анализ неопределенностей, которые всегда связаны с такой оценкой, с учетом новых концепций и математических подходов к постановке и решению подобных задач в экономике, основанных на физических и квантово-механических аналогиях [ 4], и является целью настоящей работы. Предлагаются также новые подходы к организации соревнований и новые методики ранжирования их участников.
Результаты исследования.
По способу оценки результатов соревнований виды спорта можно разделить на следующие основные группы:
-
дистанционные, гравитационные, дистанционно-гравитационные [1] - физический эталон оценки результата (высота или длина прыжка в сантиметрах, вес вытолкнутой штанги в килограммах, время в секундах, количество поднятий гири заданного веса и т. д.) ;
-
программированные [1], оценка осуществляется коллективным экспертом (жюри) по бальной системе (спортивная и художественная гимнастика, фигурное катание, спортивные танцы, синхронное плавание прыжки в воду и т. д.);
-
ситуационно-вариативные [1], игровые виды спорта и единоборства, где ранжирование осуществляется в результате встреч пар соперников той или иной системы розыгрыша;
-
альпинизм, горный туризм, сплав по горным рекам и другие экстремальные вида спорта [2, 3], где наилучший результат определяется уникальностью пройденных маршрутов, которым присваиваются определенные категории сложности, а ранжирование фактически осуществляется путем присвоения спортивных разрядов и званий, и более детально - внутренними экспертными самооценками.
1-я группа. Несмотря на то, что для первой группы видов спорта существуют, казалось бы, объективные показатели, тем не менее, результат каждого отдельного спортсмена зависит от организации соревнования, его ранга, состава участников, не говоря уже о неизбежных случайных составляющих, обусловленных как физическим и психологическим состоянием спортсмена, так и внешними факторами.
В качестве примера рассмотрим результаты забега на стометровке для условных спортсменов 1, 2, 3, 4, осуществленного парами по двум различным вариантам, приведенными в таблице 1.
Таблица 1
Варианты комплектации забегов в спринте
|
Спортивное состязание в беге на 100 м. |
|||||
|
1-й вар. |
Результат, с |
2-й вар. |
Результат, с |
||
|
Первый забег |
1 |
10,1 |
Первый забег |
1 |
10,4 |
|
2 |
10,2 |
3 |
11,1 |
||
|
Второй забег |
3 |
10,8 |
Второй забег |
2 |
10,5 |
|
4 |
10,9 |
4 |
11,2 |
||
|
Средн. по гр. |
10,5 |
Средн. по гр. |
10,8 |
||
В первом варианте, как видно из таблицы, в забегах участвовали близкие по силе участники, во втором - значительно отличающиеся, что привело к снижению как индивидуальных, так и средних по группе показателей.
Таким образом, результат оказался зависящим от организации соревнования, т. е. от процедуры измерения. Конечно, можно было бы увеличить количество забегов, по-разному комбинируя пары участников и проводя повторные забеги для исключения фактора случайности и повышения точности оценки. Однако подчеркнем, что это была бы другая процедура оценки силы участников, требующая, в частности, больше времени. При этом результаты могли бы оказаться зависящими от выносливости того или иного спортсмена, его опыта (правильное распределение сил по забегам) и т. д., т. е. соревнование выявило бы не сильнейшего спринтера и его скоростные качества, а иные физические качества, связанные с проявлением выносливости.
Представить математически описанные выше результаты удобно с помощью так называемых операторов, которые широко используются в математическом аппарате квантовой физики. Оператор вводится по аналогии с понятием обычной функции y = f (x) и представляет собой правило ![]() , по которому одной величине (функции, объекту) x ставится в соответствие другая величина (функция, объект) y:
, по которому одной величине (функции, объекту) x ставится в соответствие другая величина (функция, объект) y:
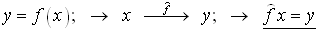 .
.
Говорят: оператор ![]() действует на x
, результат действия - y . Произведение двух операторов понимается как результат последовательного применения действий, обозначенных этими операторами:
действует на x
, результат действия - y . Произведение двух операторов понимается как результат последовательного применения действий, обозначенных этими операторами:
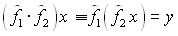 .
.
Пусть
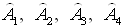 - забеги 1-го, 2-го, 3-го, 4-го спортсменов, sek1, sek2, sek3, sek4, - соответствующие им судьи с секундомерами. Тогда:
- забеги 1-го, 2-го, 3-го, 4-го спортсменов, sek1, sek2, sek3, sek4, - соответствующие им судьи с секундомерами. Тогда:
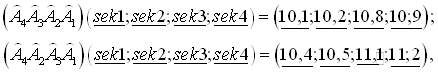
т. е. результаты зависят от порядка, в котором спортсмены выходят на дорожки. Отсюда получаем, что процедуры
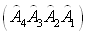 и
и 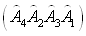 не эквивалентны:
не эквивалентны:
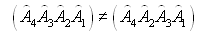
(говорят, что операторы
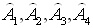 не коммутируют ).
не коммутируют ).
2-я группа. Идеальным для второй группы видов спорта (по способу оценки результатов) был бы вариант, когда один коллективный и авторитетный в данном виде спорта эксперт ("большое" жюри) оценивает всех участников состязания и принимает участие в таком качестве во всех проводимых соревнованиях.
Однако в реальности экспертов (экспертных групп) много, и чем массовее вид спорта, тем их больше. Даже в рамках одного соревнования, если участников слишком много, может возникнуть необходимость привлечения нескольких экспертных групп, или разделения имеющегося жюри на части, чтобы провести соревнование в разумные сроки. Так как эксперты по определению индивидуальности, то возникает проблема приведения разных жюри к "общему знаменателю", т. е. введение таких поправок к их оценкам, чтобы в итоге один и тот же участник, в принципе, получал одинаковые или близкие баллы у разных жюри (далее условно будем называть их "экспертами").
Итак, возможны следующие, назовем их крайними, варианты:
- один "эксперт" (это может быть и коллективный эксперт, т. е. группа экспертов со среднеарифметическим подсчетом баллов) оценивает всех n участников (n туров);
- n "экспертов", n участников, каждый "эксперт" оценивает одного участника (один тур);
- каждый из n " экспертов" оценивает каждого из n участников, результаты каждого участника усредняются по всем "экспертам" (n туров).
Как преимущества, так и недостатки каждого из этих вариантов очевидны. Мы предлагаем новый метод организации процедур измерения, суть которого проще всего пояснить на нижеследующем примере.
Рассмотрим в качестве "спортсменов" три группы студентов (n = 3 ), а в качестве "экспертов" - трех преподавателей, оценивающих ("измеряющих") их знания по данному предмету по четырехбальной системе (см. табл. 2).
Таблица 2
Варианты комплектации "экспертов" (преподавателей в группах)
|
Основные измерения и их результаты |
|||
|
Группа |
АГ-1 |
АГ-2 |
АГ-3 |
|
Преподаватель |
1 |
2 |
3 |
|
Оценки |
4-5 |
3-4 |
2-3 |
|
Дополнительные измерения и их результаты |
|||
|
Группа |
АГ-1 |
АГ-2 |
|
|
Преподаватель |
2 |
3 |
|
|
Оценки |
3-4 |
2-3 |
|
|
Корректирующие поправки и скорректированные оценки |
|||
|
Группа |
АГ-1 |
АГ-2 |
АГ-3 |
|
Коррекция |
-1 |
0 |
+1 |
|
Скорект. оценки |
3-4 |
3-4 |
3-4 |
Из основных измерений следует, что, либо группы имеют разные успеваемости, либо у преподавателей разные критерии оценки, либо имеет место, как первое, так и второе одновременно.
Сравнение двух первых основных измерений и двух дополнительных показывает, что преподаватели действительно отличаются (например, в одной и той же группе АГ-1 первый преподаватель выставил на один балл выше оценки по сравнению со вторым), и после введения корректирующих поправок оказывается, что на самом деле все группы имеют одинаковую успеваемость.
Отметим, что в нашем примере число туров (2) и общее число измерений (5) меньше, чем в крайнем варианте 3 (n = 3 тура и n2 = 9 измерений), причем эта разница в относительных единицах существенно возрастает с увеличением количества участников соревнований и "экспертов" (два тура и (2n - 1 ) измерений вместо n туров и n2 измерений в крайнем варианте 3).
Базовая идея метода состоит в том, что "эксперты" тестируют спортсменов, а спортсмены, в свою очередь, одновременно тестируют "экспертов", устанавливая их шкалы измерений с использованием минимального числа измерений при их оптимальной организации. Возможен также двухмерный (в общем случае k -мерный, с (k +1 ) турами) вариант реализации данного метода оценок. Конечно, с увеличением числа туров до n и более "теоретическая" (т. е. без учета времени проведения соревнований, усталости спортсменов и т. д. и т. п.) точность результатов возрастает, но данный подход позволяет получить оптимальные соотношения длительности соревнований и качества полученных оценок для каждого конкретного случая.
Схема взаимных относительных оценок качества "экспертов" может быть представлена в виде графа, вершины которого представляют "экспертов", а каждое ребро - относительную корректирующую поправку (набор поправок) для пары "экспертов", которых соединяет это ребро. Нахождение поправочных коэффициентов к оценке каждого эксперта связано с решением так называемых некорректно поставленных задач [5], что, с учетом возможностей современной компьютерной математики, не представляет больших проблем.
Подобные измерительные принципы фактически используются в технических (матричные цифровые фотоаппараты и видеокамеры) и биологических (зрение человека и млекопитающих) системах, и, скорее всего, работают и в механизмах рыночного установления цен.
Компьютерное моделирование работы цифрового фотоаппарата с "плохой" матрицей (матрицей из 64*64=4096 "экспертов", оценивающих элементы изображения - "спортсменов") до и после коррекции, основанной на изложенных выше идеях, представлено на рис. 1, 2, 3.

Рис. 1 - Данные для моделирования: исходное сканируемое изображение (1), коэффициенты матрицы (3) и случайные шумы ее элементов (4)
3-я группа. Третья по способу оценки результатов группа - игровые виды спорта и единоборства. Используемые в практике проведения соревнований системы можно разбить на два вида:
- системы с определенным числом туров (круговая, швейцарская и система Мак-Магона);
- системы с выбыванием (олимпийская система и ее варианты).

Рис. 2 - Три смещенных изображения (изображения (2) и (3) смещены относительно (1) на один элемент вниз и один элемент вправо соответственно), полученных матрицей без введения корректирующих поправок

Рис. 3 - Восстановленные по изображениям рис. 2 корректирующие коэффициенты (4), изображение (5) и остаточные погрешности (6). (Изображение (6) по сравнению с (4) и (5) по контрасту увеличено в 20 раз )
Что касается олимпийской системы, то она с достоверностью определяет только лидера (в предположении, что лидер не дает "сбоев" на протяжении всего турнира), но формально можно провести ранжирование и всех остальных участников турнира. Так, проигравший в финале занимает 2-е место (хотя есть вероятность p = 0,33 того, что в действительности он не 2-й, а 3-й), из двух выбывших участников полуфинала 3-е место присваивается тому, кто проиграл лидеру, а четвертое - проигравшему, занявшему 2-е место, следующие четыре места занимают участники четвертьфинала, игравшие со спортсменами, занявшими 1-е, 2-е, 3-е и 4-е места соответственно, и т. д.
Круговая система, по общепринятому мнению, позволяет наиболее объективно провести ранжирование участников соревнования, однако, нужно отметить следующее:
-
игра (состязание) по принципу "каждый с каждым" при N участниках требует проведения (N - 1 ) туров и N (N - 1) игр, что при больших N может значительно удлинить турнир (если не вообще сделать его невозможным);
-
если турнир длится достаточно долго, то его результатом может стать ранжирование игроков не столько по мастерству, сколько по выносливости;
-
в условиях длительного турнира игрок, достигший вершины своего мастерства и показывающий стабильные результаты, находится не в равных условиях с игроком, не достигшим своей спортивной формы, обладающим большим потенциалом и способным увеличивать свою игровую силу (обучаться) по мере увеличения числа сыгранных партий.
Ранжирование участников осуществляется по количеству набранных ими очков, при этом в случае равенства очков у двух и более игроков используется коэффициент Бергера, который отдает приоритет игроку, набравшему свои выигрышные очки во встречах с более сильными соперниками.
Но даже в идеальных условиях в круговом турнире присутствует фактор случайности (сила игрока от игры к игре может случайным образом колебаться, что влияет на результат), а также возможна ситуация, когда рейтинги игроков в принципе несравнимы. Если, например, в турнире с тремя участниками A,B,C игрок A стабильно выигрывает в игрока B , игрок B - в C , а последний - в A , то только формально (при любой системе подсчета приоритетов) можно считать, что силы игроков равны.
Швейцарская система используется тогда, когда число участников N значительно превосходит число возможных туров и позволяет выделить группу лидеров, близких по силе игры. С этой целью после каждого тура участники разбиваются на группы, набравшие примерно одинаковое число очков, и в следующем туре встречаются участники одной и той же группы. Если число туров достаточно велико (оптимальным считается ~ N/3 ), то результаты выделения группы лидеров и ранжирования в целом считают объективными. Для сравнения участников, набравших одинаковые очки, используют коэффициенты Бухгольца, учитывающие результаты личных встреч.
В отличие от круговой, в швейцарской системе снижается влияние фактора длительности турнира на качество ранжирования, однако, возрастают погрешности, связанные с неполным перебором игровых пар и определенным субъективизмом стратегии их формирования.
Система Мак-Магона придумана относительно недавно, уменьшает количество туров по сравнению со швейцарской и отличается от нее тем, что участники турнира, имеющие различные рейтинги по результатам предыдущих соревнований, сразу разбиваются на n групп, примерно равных по силе участников, и в первом туре спортсмены каждой группы играют между собой. При этом участники наиболее сильной группы сразу получают по (n-1 ) баллов, следующей - по (n-2 ) баллов, и т. д., наиболее слабая группа предварительных очков ("форы") не получает. Игра в последующих турах происходит по обычной, швейцарской системе.
Итак, как и в первых двух группах, результат ранжирования в третьей группе зависит от организации процедуры измерений, при этом с уменьшением ее длительности погрешность результата возрастает, однако, увеличение длительности процедуры может изменить содержание и качество измеряемых спортивных характеристик.
4-я группа. Что касается последней, четвертой группы видов спорта, то измерительные процедуры в них наименее формализованы, а, следовательно, и результаты измерений обладают наибольшей неопределенностью.
Выводы .
1. Проведенный анализ показывает, что для всех видов спорта и во всех способах оценки результатов присутствует принципиально неустранимая неопределенность, обусловленная влиянием процедуры измерений на результат. Эта неопределенность имеет аналогию с релятивистским принципом неопределенности в квантовой механике, который можно записать в виде:
(Время измерения)*(предельная погрешность) ~ const.
2. Использование квантово-механических аналогий (в том числе принципа неопределенности и понятия оператора) в социально-экономических процессах является предметом рассмотрения нового междисциплинарного направления - квантовая эконофизика [4]. Применение подобного подхода к проблеме измеримости в спортивной педагогике и состязаниях, как видно из вышеизложенного, может оказаться естественным и весьма плодотворным.
3. Практическая значимость результатов данной работы состоит в том, что предложенные подходы и алгоритмы могут быть использованы для отработки новых схем организации соревнований, прежде всего массовых, а также для извлечения дополнительной информации из банка данных, касающихся уже проведенных соревнований.
Дальнейшие исследования необходимо сосредоточить на усовершенствование систем соревнований в отдельных видах спорта с учетом проблем затронутых в статье.
Литература
1. Ивойлов А.В. Соревнования и тренировка спортсмена / Ивойлов А. В. - Минск: Вышэйша школа, 1982. - 144 с.
2. Келлер В.С. Система спортивных соревнований и соревновательная деятельность спортсмена // Теория спорта. - К.: Вища шк., 1987. - С. 66 - 100.
3. Платонов В.П. Общая теория подготовки спортсменов в олимпийском спорте / Платонов В. П. - К.: Олимпийская литература, 1997. - 583 с.
4. Соловьев В.Н. Квантовая эконофизика - физическое обоснование системных концепций в моделировании социально-экономических процессов / В.Н. Соловьев, В.М. Сапцин: материалы II Международной Школы-симпозиума АМУР - 2008 ["Анализ, моделирование, управление, развитие экономических систем"], (Севастополь, 12-18 сент. 2008 г.) / отв. ред. О. Л. Королева, А. В. Сигал. - Симферополь, 2008. - С. 94 -102.
5. Тихонов А.Н. Методы решения некорректных задач / Тихонов А.Н. - М.: Наука, 1986. - 288 с.
Поступила в редакцию 12 .11.2009 г.
Сапцин Владимир Михайлович
Циповьяз Анатолий Тимофеевич
saptsin@sat.poltava.ua