ИСПОЛЬЗОВАНИЕ ВЫБОРОЧНОГО МЕТОДА ДЛЯ АНАЛИЗА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ В СПОРТИВНО-ПЕДАГОГИЧЕСКОЙ ПРАКТИКЕ
Усыченко В.В., Бышевец Н.Г.
Национальный университет физического воспитания и спорта Украины
Аннотация. В статье рассматриваются статистические методы, используемые в спортивно-педагогической практике на примере анализа антропометрических показателей спортсменов-бодибилдеров высокой квалификации на соревновательном этапе подготовки.
Ключевые слова. Выборочная совокупность, генеральная совокупность, вариация, средняя ошибка выборки, предельная ошибка выборки, среднеквадратическое отклонение.
Анотацiя. Усиченко В.В., Бишевець Н.Г. Використання вибiркового методу для аналiзу результатiв вимiрювань в спортивно-педагогiчнiй практицi. В статтi розглядаються статистичнi методи, що використовуються в спортивно-педагогiчнiй практицi на прикладi аналiзу антропометричних показникiв спортсменiв-бодибiлдерiв високоi квалiфiкацii на змагальному етапi пiдготовки.
Ключовi слова. Вибiркова сукупнiсть, генеральна сукупнiсть, варiацiя, середня похибка вибiрки, гранична похибка вибiрки, середньоквадратичне вiдхилення.
Annotation. Usychenko V.V., Bishevets N.G. Use of the selective method for the analysis of results of measurements in is sports-student teaching. This paper considered the statistical methods which used in sports and pedagogical practice student teaching on an example of the analysis of anthopometrical parameters of high skilled bodybuilders at a competitive stage of training.
Keywords. A sample, general set, a variation, an average error of sample, a limiting error of sample, standard a deviation.
Введение.
Построение эффективного тренировочного процесса является фундаментальной задачей современного спорта. При организации учебно-тренировочного процесса, тренеру поступает огромное количество числовой информации. Для ее изучения и систематизации, выявления взаимосвязей и закономерностей между рассматриваемыми признаками и явлениями, создания на этой основе рациональных технологий спортивной тренировки, научного подхода к прогнозированию спортивных достижений, тренеру необходимо задействовать инструменты и методы математической статистики. В связи с этим получил широкое распространение процесс внедрения количественных методов, использующих математический аппарат в сферу физического воспитания и спорта [1,4]. При разработке методики спортивной тренировки исследователь реализует свои идеи на конкретной, обычно немногочисленной группе спортсменов. Особенность научного подхода к подготовке спортсменов высокой квалификации заключается в том, что использование тренером неадекватного метода анализа результатов измерений даже на одном из этапов работы лишает его выводы достоверности. Становится очевидным, что спортивная практика претендует на решение задачи, где информацию, полученную на малом количестве объектов желательно перенести на большую группу объектов, известная в математической статистике как выборочный метод.
Современный спорт высших достижений характеризуется постоянным увеличением количества показателей, отражающих тренировочно-соревновательный процесс, а определение физического развития спортсменов является неотъемлемой частью их комплексного обследования. Учитывая специфичность адаптационных изменений в организме, специалисты предполагают и специфичность морфометрических характеристик у спортсменов в зависимости от вида спорта. Можно утверждать, что информация об особенностях физического развития спортсменов в определенном виде спорта имеет как теоретическое значение, так и возможность использовать эти данные в процессе практической работы. Дать реальную оценку большим массивам информации, тщательно проанализировать ее, сделать научно обоснованные выводы помогают методы математической статистики [2].
Средства и методы математической статистики оказывают серьезную помощь в спортивных исследованиях. По оценкам специалистов, при помощи характеристик вариационных рядов можно провести анализ какого-либо процесса, необходимый для управления тренировкой [4]. Самым характерным и существенным параметром вариационного ряда является средняя арифметическая величина, которая показывает средний уровень всех измерений для данной группы чисел. Однако в процессе исследования спортсменов высокой квалификации, тренер не имеет возможности составить выборку такой численности, которая бы по своему объему отвечала закону больших чисел. По оценкам Начинской С.В., достаточно репрезентативной следует считать выборку из 30 объектов [4]. С другой стороны, Орехов Л.И. с соавторами утверждает, что правомерными могут быть и единичные наблюдения за выдающимися спортсменами: регистрация множества показателей в динамике в течение длительного времени дают ценный материал, который при компетентном анализе может помочь выявить важные закономерности, уточняющие существующие положения в физическом воспитании и спорте [5]. В других публикациях Л.И. Орехов отмечает, что игнорирование специалистами современного понимания статистических и экспериментальных методов отрицательно отражается на эффективности научных исследований [6].
Таким образом, анализ научно-методической и специальной литературы свидетельствует, что актуальность вопросов о применении методов математической статистики в исследовании задач, связанных с проблемами подготовки спортсменов высокой квалификации является очевидной и не вызывает сомнений.
Работа выполнена по плану НИР Национального университета физического воспитания и спорта Украины.
Формулирование целей работы.
Цель работы - анализ применения методов математической статистики в исследовании задач, связанных с проблемами подготовки спортсменов высокой квалификации.
Результаты исследований.
В связи с тем, что объем выборки всегда меньше объема генеральной совокупности, и, как следствие, средняя выборки не может быть точно равна средней генеральной, для определения средней арифметической генеральной совокупности без исследования всех объектов ее объема, математическая статистика предлагает выборочный метод. Рассмотрим использование выборочного метода для изучения результатов измерений в спортивно-педагогической практике на примере анализа охватных размеров бодибилдеров высокой квалификации на соревновательном этапе подготовки.
В результате измерений антропометрических показателей спортсменов-бодибилдеров, участвовавших в чемпионате Украины 2004, кубке Украины 2004, чемпионате Украины 2005 года, а также на основании сведений, полученных в ходе исследований, проведенных на базе научно-исследовательского института НУФВСУ, нами получены данные, представленные в таблице 1 (табл.1).
Таблица 1.
Антропометрические показатели спортсменов - бодибилдеров высокой квалификации на соревновательном этапе подготовки
|
№ |
Возраст |
Рост |
Масса |
Обхват бицепсов |
Обхват предплечья |
Обхват грудной клетки |
Талия |
Обхват бедра |
Обхват голени |
||||
|
А |
В |
А |
В |
А |
В |
А |
В |
||||||
|
До 80 кг, n=4 |
|||||||||||||
|
1 |
37 |
160 |
80 |
46 |
47 |
35 |
34 |
130 |
68 |
66 |
65 |
45 |
44 |
|
2 |
24 |
171 |
80 |
42 |
41 |
32 |
32 |
125 |
75 |
55 |
55 |
43 |
43 |
|
3 |
19 |
163 |
73 |
43 |
44 |
32 |
31 |
110 |
73 |
54 |
54 |
42 |
43 |
|
4 |
23 |
170 |
75 |
40 |
40 |
31 |
30 |
110 |
72 |
58 |
58 |
41 |
41 |
|
До 90 кг, n=4 |
|||||||||||||
|
1 |
28 |
163 |
85 |
47 |
47 |
38 |
38,5 |
125 |
60 |
68 |
69 |
44 |
44 |
|
2 |
31 |
168 |
86 |
49 |
50 |
40 |
39 |
136 |
85 |
70 |
70 |
45 |
44,5 |
|
3 |
28 |
171 |
87 |
48 |
47,5 |
37 |
38 |
135 |
83 |
69 |
70 |
44 |
44 |
|
4 |
22 |
180 |
90 |
48 |
48 |
43 |
43 |
130 |
76 |
71 |
71 |
46 |
46 |
|
Свыше 90 кг, n=4 |
|||||||||||||
|
1 |
28 |
184 |
113 |
54 |
53,5 |
41 |
41,5 |
146 |
94 |
78 |
79 |
48 |
48 |
|
2 |
27 |
178 |
95 |
50 |
50 |
40,5 |
41 |
139 |
89 |
72 |
73 |
45 |
45 |
|
3 |
40 |
185 |
102 |
48 |
48 |
38 |
38 |
130 |
91 |
67 |
67 |
44 |
43,5 |
|
4 |
32 |
180 |
94,5 |
48 |
48 |
37 |
37 |
135 |
79 |
65 |
65 |
42 |
42 |
|
5 |
36 |
173 |
94,6 |
47 |
47,5 |
38 |
38 |
136 |
88 |
67 |
68 |
42 |
43 |
|
6 |
22 |
180 |
103 |
48 |
48 |
43 |
43 |
130 |
89 |
70 |
70 |
46 |
46 |
|
7 |
29 |
173 |
99 |
48 |
48 |
43 |
43,2 |
132 |
74 |
73 |
73 |
48 |
48 |
Для полного отражения результатов измерения антропометрических данных бодибилдеров высокой квалификации в исследуемых группах, были определены параметры вариационных рядов, составленных из охватных размеров спортсменов. Для этого были вычислены средние значения обхватов спортсменов, используя формулу:
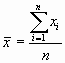 (1),
(1),
где n - объем выборки.
Согласно рекомендациям специалистов [2,4,6], стандартное отклонение в случае малых выборок (n<30), отражающее вариативность обхватов спортсменов, вычислено по следующей формуле:
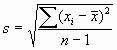 (2).
(2).
Для расчета ошибок выборок небольшого объема используется специфический математический аппарат: средняя ошибка малой выборки вычисляется по формуле
![]() (3),
(3),
где s - средне квадратическое отклонения в генеральной совокупности по малой выборке.
Чтобы отразить вариативность обхватов в процентах, был рассчитан коэффициент вариации:
![]() (4).
(4).
В процессе исследования полученных результатов, нами были изучены все антропометрические показатели. Рассмотрим их на примере анализа обхвата правого бицепса (А) спортсменов в категориях до 80 и до 90 кг.
По результатам вычислений, в категории до 80 кг средний обхват правого бицепса составил 42,8 см, а у спортсменов категории до 90 кг соответственно 48 см. Находим средние ошибки каждой выборочной совокупности:
![]() см,
см,
![]() см.
см.
Из этого следует, что средний обхват бицепсов у спортсменов категории до 80 кг составляет
![]() 42,8 ±1,11 см, а соответственно у спортсменов категории до 90 кг-
42,8 ±1,11 см, а соответственно у спортсменов категории до 90 кг-
![]() 48±0,41см.
48±0,41см.
Средняя ошибка выборки дает некоторое представление об ошибке репрезентативности, то есть об ошибке, с которой выборочная средняя представляет действительное значение генеральной средней. Однако в каждой конкретной выборке ошибка может существенно отличаться от средней ошибки [3]. Следует отметить, что нет гарантии, что ошибка, которая действительно была допущена в конкретном выборочном исследовании, не превышает средней ошибки. Поэтому гораздо полезнее знать те границы, в которых "практически наверняка" находится действительная ошибка, допущенная в данной конкретной выборке. Эти границы указываются предельной ошибкой выборки, которая вычисляется по формуле:
![]() (4),
(4),
где t рассчитывают исходя из так называемого закона распределения Стьюдента с k степенями свободы (в отличие от больших выборок, где t вычисляется на основе нормального закона распределения) [5]. При вычислении предельной ошибки малой выборки значение t(k) определяем по таблице значения критерия Стьюдента с k =
n-1 степенями свободы, с учетом заданного уровня надежности и объема выборки. Задавшись уровнем надежности
P = 0.95, находим ![]() . Тогда предельные ошибки выборок:
. Тогда предельные ошибки выборок:
![]()
![]() .
.
Исходя из полученных результатов, для спортсменов категории до 80 кг границы обхвата бицепса в генеральной совокупности составляют
39,01 < x1 < 46,59 см,
а для спортсменов категории до 90 кг - 46,7 <
x1 < 48,3 см.
Аналогичным образом находим средние и предельные ошибки каждой выборочной совокупности по каждому показателю (табл.2).
Таблица 2.
Анализ средних показателей для малых выборок спортсменов различных весовых категорий
|
Показатели |
Обхват бицепсов |
Обхват предплечья |
Обхват грудной клетки |
Талия |
Обхват бедра |
Обхват голени |
||||
|
А |
В |
А |
В |
А |
В |
А |
В |
|||
|
До 80 кг |
||||||||||
|
|
42,8 |
43 |
32,5 |
31,8 |
118,8 |
72 |
58,3 |
58 |
42,8 |
42,8 |
|
s |
2,38 |
2,14 |
2,46 |
2,55 |
5,71 |
7,11 |
4,46 |
4,72 |
2,52 |
2,39 |
|
V |
5,85 |
7,35 |
8,68 |
3,99 |
2,94 |
9,34 |
8,56 |
5,33 |
5,38 |
4,09 |
|
|
1,19 |
1,07 |
1,23 |
1,28 |
2,86 |
3,56 |
2,23 |
2,36 |
1,26 |
1,20 |
|
|
3,79 |
3,40 |
3,91 |
4,06 |
9,08 |
11,31 |
7,10 |
7,51 |
4,01 |
3,80 |
|
До 90 кг |
||||||||||
|
|
48 |
48,1 |
39,5 |
39,6 |
131,5 |
76 |
69,5 |
70 |
44,75 |
44,6 |
|
s |
0,82 |
1,31 |
2,65 |
2,29 |
5,07 |
11,34 |
1,29 |
0,82 |
0,96 |
0,95 |
|
V |
1,70 |
2,73 |
3,85 |
2,14 |
2,12 |
1,86 |
1,17 |
6,70 |
5,77 |
14,93 |
|
|
0,41 |
0,66 |
1,33 |
1,15 |
2,54 |
5,67 |
0,65 |
0,41 |
0,48 |
0,48 |
|
|
1,30 |
2,08 |
4,22 |
3,64 |
8,07 |
18,04 |
2,05 |
1,30 |
1,53 |
1,51 |
|
Свыше 90 кг |
||||||||||
|
|
49 |
49 |
40,1 |
40,2 |
135,4 |
86,2 |
70,3 |
70,7 |
45 |
45,1 |
|
s |
2,50 |
3,16 |
1,73 |
1,71 |
10,31 |
2,94 |
5,44 |
4,97 |
1,71 |
1,26 |
|
V |
4,86 |
4,37 |
4,22 |
5,59 |
5,30 |
6,35 |
6,67 |
6,13 |
6,34 |
8,25 |
|
|
0,94 |
1,19 |
0,65 |
0,65 |
3,90 |
1,11 |
2,06 |
1,88 |
0,65 |
0,48 |
|
|
2,23 |
2,82 |
1,55 |
1,53 |
9,21 |
2,63 |
4,86 |
4,44 |
1,53 |
1,13 |
Выводы.
Изучение научно-педагогической и специальной литературы, а также результаты использования выборочного метода для оценки средних параметров генеральной совокупности на примере анализа охватных размеров спортсменов-бодибилдеров высокой квалификации разных весовых категорий, позволили сделать следующие выводы:
1. Выборочный метод позволяет оценить средние показатели генеральной совокупности в случае ограниченного количества испытаний. Найденные ошибки репрезентативности фактически указывают на то, как отличаются средние арифметические генеральной совокупности от найденных с помощью выборочной совокупности величин.
2. Вычисление коэффициентов вариации для каждого из показателей, позволило констатировать, что исходя из результатов расчетов, согласно которым коэффициенты вариации не превышают 15%, группы спортсменов в зависимости от весовой категории однородны и однотипны.
3. При сопоставлении полученных результатов установлено, что средние охватные размеры спортсменов увеличиваются с увеличением их весовой категории. Однако такой вывод пока еще неправомерен и может рассматриваться лишь как гипотеза в связи с тем, что доверительные интервалы для генеральных средних отдельных показателей бодибилдеров (например, интервал обхвата правого предплечья в весовой категории до 80 кг составляет от 28,59 до 36,41, а соответственный интервал для обхвата правого предплечья спортсменов категории до 90 кг - от 35,28 до 43,72) пересекаются, так что средние генеральные вполне могут совпадать или даже находиться в соотношении, противоположном высказанной гипотезе. Поэтому, чтобы попытаться подтвердить и обосновать высказанную выше гипотезу следует значительно увеличивать объем выборок. Тем не менее, можно утверждать, что охватные размеры спортсменов различны в зависимости от весовых категорий по следующим показателям:
- для спортсменов категорий до 80 и до 90 кг гипотеза справедлива для обхвата правого бицепса (А), левого предплечья (В) и обхвата обоих бедер;
- для спортсменов категорий до 90 и свыше 90 кг для подтверждения или опровержения гипотезы необходимы дополнительные исследования;
- для спортсменов категорий до 80 и свыше 90 кг зафиксированное различие обхвата правого бицепса (А), правого и левого предплечья, обхвата талии и обоих бедер бодибилдеров высокой квалификации имеет не случайный, а закономерный характер.
Дальнейшее исследование направить на изучение статистических методов, позволяющих определить различия между средними показателями в случаях малых выборок на примере анализа антропометрических данных спортсменов-бодибилдеров высокой квалификации в соревновательном периоде.
Литература
1. Губа В.П., Шестаков М.П., Бубнов Н.Б., Борисенко М.П. Измерения и вычисления в спортивно-педагогической практике.- Учебное пособие.- СпортАкадемпресс.- 2002.- 211с.
2. Мiстулова Т.Е. Математичнi методи в теорii та практицi спорту: Навч. посiб.- К.:Наук. Свiт, 2004.-90с.
3. Лакин Г.Ф. Биометрия. - "Высшая школа".- Москва.- 1973.- 342с.
4. Начинская С.В. Математическая статистика в спорте.- Киев "Здоров’я".- 1978.- 134с.
5. Орехов Л.И., Караваева Е.Л., Асмолова Л.А. Управление, контроль, измерение, статистические и экспериментальные методы в педагогике, психологии и физической культуре. - Учебное пособие.- Алматы.- 2004.- 168с.
6. Орехов Л.И., Караваева Е.Л. О необходимости соответствия статистических и экспериментальных методов современным требованиям // Теор. и практика физ. культуры. - 2005.- №3.- С. 46-49.
Поступила в редакцию 11.11.2006г.