МЕТОД ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ ЦЕНТРА МАСС И ОСЕВЫХ МОМЕНТОВ ИНЕРЦИИ ТЕЛА ЧЕЛОВЕКА
Адашевский В.М., Андреев Ю.М.
Национальный технический университет <ХПИ>
Аннотация. В статье предложен экспериментально-теоретический метод определения положения центра масс и моментов инерции тела человека относительно трех анатомических осей при помощи специального стенда, представляющего жесткий тетраэдр.
Ключевые слова: центр масс, тензор инерции, оси координат, тетраэдр.
Анотацiя. Адашевский В.М., Андреев Ю.М. Метод визначення положення центра мас i осьових моментiв iнерцii тiла людини. У статтi запропонований експериментально-теоретичний метод визначення положення центра мас i моментiв iнерцii тiла людини щодо трьох анатомiчних осей за допомогою спецiального стенда, що представляе жорсткий тетраедр.
Ключовi слова: центр мас, тензор iнерцii, осi координат, тетраедр.
Annotation. Adashevskii V.M., Andreev Y.M. Method of determination of position of a center of mass and axial moments of inertia of a skew field of the person. In the article the experimentally - idealized method of determination of position of a center of mass and moments of inertia of a body of the person concerning three anatomical axes is offered through a special bench presenting a rigid tetrahedron.
Keywords: center of mass, tensor of inertia, axes of coordinates, tetrahedron.
Введение.
Для повышения эффективности спортивных действий связанных с вращением тела человека и их математического моделирования необходимо определить положение центра масс, а также осевые моменты инерции тела.
Известны различные экспериментальные методы для определения положения центра масс и моментов инерции твердых тел [1,2].. Эти методы, возможно, использовать для определения положения центра масс и моментов инерции тела человека относительно трех анатомических осей при различных его позах и ориентациях тела в пространстве.
Одним из таких экспериментальных методов является метод колебаний. Например, для определения значения момента инерции тела человека относительно фронтальной оси, изучают колебания физического маятника, роль которого выполняет система "человек-качели". В этом случае плоскость качелей совпадает с фронтальной плоскостью тела человека. Если провести те же опыты, изменив ориентацию тела, поворотом его на 90° относительно продольной оси, то можно определить значение момента инерции тела человека относительно сагиттальной оси.
Изменив ориентацию тела, поворотом его на 90° относительно сагиттальной оси, возможно, определить момент инерции человека относительно продольной оси.
В других опытах для определения значений моментов инерции тела человека относительно тех же анатомических осей в различных позах при различных ориентациях тела, изучаются крутильные колебания платформы в форме диска, подвешенной на нескольких тросах (многофилярный подвес) и системы "человек - платформа".
Координаты центра масс тела человека затем находится по соответствующим математическим зависимостям с использованием теоремы Гюйгенса
Для определения положения центра масс тела человека используют также динамометрические платформы.
Платформа может быть различной геометрической формы. Например, ее конструкция может иметь форму равностороннего треугольника, горизонтальная плоскость которой опирается в трех угловых точках на динамометры.
Располагая человека на платформе в исследуемой позе, определяют проекции центра масс (центра тяжести) тела, на горизонтальную плоскость платформы, используя уравнения статики.
Уравнения статики представляют алгебраические суммы моментов весов платформы, тела человека и реакций сил в опорных точках, полученных из показаний динамометров.
В этом случае находится точка пересечения отрезков (плечей сил) от соответствующих осей до проекции центра масс.
Изменяя неоднократно ориентацию тела по отношению к соответствующим осям возможно определить пространственное положение центра масс.
Указанные выше экспериментальные методы имеют существенные недостатки. В частности при изменении ориентации относительно трех анатомических осей трудно сохранить неизменной позу испытуемого человека, а это может привести к значительным погрешностям значений результатов эксперимента.
Работа выполнена по плану НИР Национального технического университетв Украины "ХПИ".
Формулирование целей работы.
Цель работы - создание рационального способа и методики определения положения центра масс и осевых моментов инерции тела человека относительно его анатомических осей.
Результаты исследования.
Предлагается способ, позволяющий полностью найти весь тензор инерции и положение центра масс твердого тела осуществлением небольшого числа простых опытов. Для этого можно создать специальный стенд по определению указанных характеристик. Для определения тензора инерции предлагается изготовить жесткую стержневую конструкцию в виде тетраэдра (см. рис.1), которая позволяла бы надежно закреплять в ней испытуемого человека, а также прокачивать ее вокруг осей всех шести стержней. Такой стенд дает возможность в одном цикле экспериментов получить и координаты центра масс, и тензор инерции тела.. Основы такой методики экспериментов и вычислений рассматривались в [3].
Предлагается более рациональный метод, где в настоящей измененной конструкции ребра тетраэдра располагаются специальным образом. Три ребра (I, II, III на рис. 1) одинаковой длины l, располагаются взаимно перпендикулярно. С ними связывается система координат стенда OXYZ, оси которой совпадают с анатомическими осями: OX - с фронтальной, OY- с сагиттальной, OZ - с продольной.
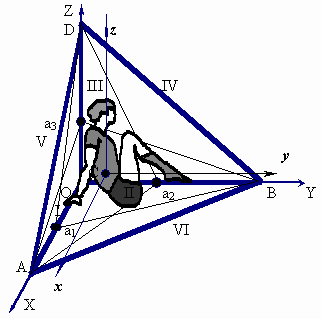
Рис. 1. Специальный стенд.
Вначале определяется положение центра масс самого стенда (без испытуемого человека). Для этого конструкция последовательно подвешивается на ребрах IV, V и VI так, чтобы опорное ребро было горизонтально, конструкция свободно находилась под ним, а способ крепления допускал поворот и качание конструкции вокруг оси подвеса. После успокоения колебаний, на ребре, противоположном опорному ребру, фиксируется точка, расположенная вертикально под опорным ребром (например, с помощью отвеса). Таким образом, определятся три точки, на рис.1. они отмечены a1, a2, a3 (так же обозначим и расстояния этих точек от начала координат). Точка пересечения трех плоскостей, образованных этими точками и соответствующими им осями подвеса (ребрами) будет центром тяжести всей механической системы. Для вычисления координат центра тяжести человека необходимо произвести такие же эксперименты для тетраэдра с закрепленным внутри него объектом (человеком).
Уравнения центральных плоскостей, занимающих вертикальные положения при указанных подвесах стенда (показанных на рис. 1 осевыми линиями) получаются по координатам трех точек на осях координат [4]
![]() (1)
(1)
Рассматривая эти уравнения как систему уравнений, разрешая относительно координат x, y, z, получим координаты центра тяжести стенда или координаты центра тяжести системы "стенд и объект". В первом случае в качестве координат точек a1, a2, a3 следует взять координаты этих точек при подвешивании без испытуемого объекта, а во втором - координаты в экспериментах с объектом.
Координаты центра тяжести (центра масс) объекта найдутся из разности статических моментов системы "стенд и объект" и системы "стенд"
![]() , (2)
, (2)
где m - масса объекта, ![]() - масса, а
- масса, а
![]() - координаты центра тяжести конструкции вместе с крепежом объекта, но без него,
- координаты центра тяжести конструкции вместе с крепежом объекта, но без него,
![]() - координаты общего центра масс - конструкции и закрепленного в ней объекта.
- координаты общего центра масс - конструкции и закрепленного в ней объекта.
Момент инерции тела относительно некоторой произвольной оси
![]() можно записать как показано в [1]
можно записать как показано в [1]
![]() (3)
(3)
Здесь ![]() - осевые и центральные центробежные моменты инерции тела,
- осевые и центральные центробежные моменты инерции тела,
![]() - направляющие косинусы данной оси
- направляющие косинусы данной оси
![]() с осями координат
с осями координат
![]() соответственно,
m - масса тела, d - расстояние от центра масс до оси.
соответственно,
m - масса тела, d - расстояние от центра масс до оси.
На этом основании по экспериментально определенным шести моментам инерции стенда вместе с телом относительно всех шести ребер тетраэдра получим систему уравнений для вычисления центральных моментов инерции тела
![]() (см. рис. 1).
(см. рис. 1).
Расстояния центра масс от ребер и моменты инерции тела относительно ребер
![]()
![]()
![]()
![]() (4)
(4) ![]()
![]()
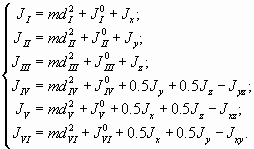 (5)
(5)
Здесь ![]() - моменты инерции стенда относительно ребер без испытуемого тела, но с крепежом - определяются заранее до установки тела на стенде. Фиксируя периоды малых колебаний установки вокруг положений устойчивого равновесия при подвешивании ее на каждом из ребер, можно найти моменты инерции из левых частей равенств (5) по формулам
- моменты инерции стенда относительно ребер без испытуемого тела, но с крепежом - определяются заранее до установки тела на стенде. Фиксируя периоды малых колебаний установки вокруг положений устойчивого равновесия при подвешивании ее на каждом из ребер, можно найти моменты инерции из левых частей равенств (5) по формулам
![]() , где j - номер ребра тетраэдра,
, где j - номер ребра тетраэдра,
![]() - период малых колебаний конструкции с испытуемым объектом вокруг соответствующего ребра. Решение системы (5) позволяет найти значения искомых моментов
- период малых колебаний конструкции с испытуемым объектом вокруг соответствующего ребра. Решение системы (5) позволяет найти значения искомых моментов![]() .
.
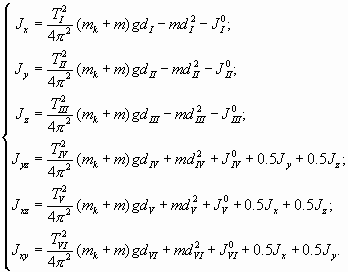 (6)
(6)
Вывод:
Описанный в статье метод позволит определять рациональным способом положение центра масс и значения осевых моментов инерции тела человека для любых его поз и ориентаций в пространстве с высокой точностью и малыми затратами времени на эксперимент.
Дальнейшие исследования предполагается провести в направлении изучения других проблем определения положения центра масс и осевых моментов инерции тела человека.
Список литературы
1. Фаворин М.В. Моменты инерции тел. Справочник /Под ред. М.М.Гернета. Изд. 2-е. - М., 1977. 512 с.
2. Гернет М.М., Ратобыльский B.И. Экспериментальное определение моментов инерции
3. Андреев Ю.М., Шелудяков О.Л. Рациональный метод экспериментального определения тензора инерции звеньев пространственных механизмов. Вестник ХГПУ, вып. 29, 1999, 7с.
4. Бронштейн И.Н., Семендяев К.А. Справочник по математике. М., 1964., 608с.
Поступила в редакцию 10.05.2005г.