ВОЗМОЖНОСТИ НЕПАРАМЕТРИКИ В СПОРТЕ*
В. Ткачук1, Б. Петрович1, А. Раковски1, Я. Сковрон1, А. Здешиньски1, В. Ягелло2, T. Poliszczuk3, А. Ойжановски4, Т. Ясински5
1- Кафедра гимнастики, 2- Кафедры спортивной борьбы и тяжелой атлетики,
3-Теории спорта, 4- Спортивных игр
Институт СпортаАкадемии физического воспитания Ю. Пилсудского в Варшаве
5- Лаборатория летной психологии Военного института летной медицины
Анотация. В. Ткачук, Б. Петрович, А. Раковски, Я. Сковрон, А. Здешиньски, В. Ягелло, T. Полищук, А. Ойжановски, Т. Ясиньски. Возможности непараметрики при анализе данных в спорте. Работа посвящена анализу возможностей статистики при индивидуальной организации учебно-тренировочного процесса элитных спортсменов.
Ключевые слова: спорт, статистический анализ
Анотацiя. В. Ткачук, Б. Петровiч, А. Раковскi, Я. Сковрон, А. Здешиньскi, В. Ягелло, T. Полiщук, А. Ойжановскi, Т. Ясиньскi. Можливостi непараметрикi при аналiзi даних у спортi. Праця присвячена аналiзу можливостей статистики пiд час iндивiдуальноi органiзацii навчально-тренувального процесу спортсменiв.
Ключовi слова: спорт, статистичний аналiз.
Annotation. V. Tkachuk, B. Petrowicz, A. Rakowski, W. Jagiello, T. Poliszczuk, A. Ojrzanowski, Ja. Skowron, A. Zdzieszyński, T. Jasiński. Possibilities non-parametric at a data analysis in sports. The work is dedicated to analysis of possibilities of a statistician at personal architecture of the trainer process of the elite sportsmen.
Key words: sport, statistical analysis.
___________________
* Работа выполнена в соответствии с планом НИР АФВ в Варшаве - Ш-92.
Проблемная ситуация
Не секрет, что статистика является очень важной дисциплиной весьма широко используемой при анализе разнообразных явлений в природе и обществе. Она так широко и долго применяется человечеством, что многие ее постулаты и методы принимаются как аксиомы - без доказательств равно как специалистами, так и рядовыми пользователями. Между тем, как и любая другая научная и прикладная дисциплины, статистика не стоит на месте, а находится в постоянном развитии и совершенствовании. И в этом плане интересная статья А.Н. Орлова [23] натолкнула нас на написание данной работы.
В статье А.И. Орлова [23] приводятся примеры успешного использования методов статистики при решении практических задач. Подобных работ имеется огромное множество [9, 10, 14, 15 и мн. др.].
Роль статистики в практической деятельности человека такова, что она оправдывает дальнейшие разработки по ее методологии и по разнообразным прикладным направлениям.
Этапными работами в становление новых направлений в статистике - стала теория вероятностей (Паскаль, Ферма, 17 век). Эта теория привела к тому, что разнообразные математические модели стали использоваться при анализе статистических данных.
Этапным был 1794 г., когда К. Гаусс создал один из самых популярных статистических методов - "метод наименьших квадратов" [13].
Современный этап развития прикладной статистики начался с 1900 г., когда К. Пирсон начал выпускать журнал "Biometrika".
В первой трети ХХ в. доминировали методы параметрической статистики. Тогда широко использовались нормальное распределение, критерии Пирсона, Стьюдента и Фишера. Были так же внедрены метод максимального правдоподобия, дисперсионный анализ и заложены основы идеи планирования эксперимента. Следует отметить, что к перечисленным методам статистики имелись серьезные замечания, предъявленные еще в 1928 году С.Н. Бернштейном [2]. Но, к сожалению, консерватизм преподавателей в прошлом приводил и в настоящее время приводит к тому, что эти теории остаются основой преподавания статистических методов в высшей школе.
Анализ более 100.000 публикаций в сфере прикладной статистики показал А.И. Орлов [17, 19, 21], что в реальной жизни специалист может познакомиться со значительно меньшим количеством работ и, вследствие этого, владеет лишь небольшой частью существующих в текущее время знаний. Среди специалистов (и не только по статистике) существует миф о том, каждый новый результат, полученный исследователем - это кирпичик в непрерывно растущее здание науки. Чисто теоретически предполагается, что он обязательно будет проанализирован и использован соответствующими специалистами. В реальной жизни это далеко не так. А начинается реальность уже в период обучения в вузе, когда базовые профессиональные знания будущего специалиста только закладывается.
В этот период проблемы начинаются с подготовки и тиражирования знаний (учебных пособий, учебников, практикумов) для нового поколения специалистов. Из опыта такой работы известно, что вузовские учебники отстают от современного им состояния развития данной отрасли на десятки лет. Так, например, по экспертной оценке А.И. Орлова [21] учебники по математической статистике соответствуют 40-60-м годам ХХ в. Тем же годам соответствует и большинство вновь публикуемых исследований и, тем более, - прикладных работ. Как отмечает автор результаты, не вошедшие в учебники, независимо от их ценности остаются невостребованными или забываются. Это обстоятельство еще больше усугубляет негативную сторону проблемы обучения специалиста.
Исходя из сказанного, авторы на основе анализа литературы, хотели бы показать "точки развития" прикладной статистики, тех ее направлений, которые представляются перспективными как в недалеком, так и отдаленном будущем, но пока отодвинутыми на задний план традиционными решениями.
На современном этапе развития статистических методов А.И. Орловым [21] приводятся такие актуальные направления развития современной прикладной статистики:
- непараметрика,
- робастность,
- бутстреп,
- интервальная статистика,
- статистика объектов нечисловой природы.
Непараметрическая статистика
В первой трети ХХ в., одновременно с параметрической статистикой, в работах Кендaлла М.Г. [35, 36] появились первые непараметрические методы, основанные на коэффициентах ранговой корреляции. Но непараметрические методы, которые не делают нереалистических предположений о том, что функции распределения результатов наблюдений принадлежат тем или иным параметрическим семействам распределений, стала признаваться только во второй трети ХХ века. В 30-е годы появились работы А.Н. Колмогорова и Н.В. Смирнова [22], вводивших статистические критерии, которые получили их имена. Эти критерии основаны на использовании эмпирического процесса - разности между эмпирической и теоретической функциями распределения, умноженной на квадратный корень из объема выборки.
В дальнейшем развитии непараметрической статистики значительную роль сыграли работы школы Вилкоксона. Практическим результатом ее деятельности было то, что с помощью непараметрических методов можно было решать те же задачи, что и параметрических [30]. Между тем параметрические методы до настоящего времени всё еще остаются популярными. В специальной литературе много раз были показаны [20] экспериментальные данные, которые свидетельствовали о том, что распределения реальных случайных величин в преимущественно отличаются от нормальных. Тем не менее большинство специалистов из разных областей знаний продолжают изучать статистические модели, основанные на распределении гаусса.
Робастность
Теоретические предпосылки статистических методов гласят, что в параметрических задачах к исходному массиву первичных данных необходимо использовать жесткие требования, связанные с тем, что функции их распределения должны принадлежать определенному параметрическому семейству. В непараметрических методах, противоположное - излишне слабые и требующие только того, чтобы функции распределения были непрерывны.
А.И. Орлов [22] считает, что такой учет "примерного вида" распределения улучшит показатели качества статистических процедур. Развитием этой идеи является теория устойчивости (робастности) статистических процедур, в которой предполагается, что распределение исходных данных мало отличается от некоторого параметрического семейства.
Существует значительное разнообразие моделей робастности. Наиболее употребляемой оказалась модель выбросов [29, 31], в которой исходная выборка "засоряется" малым числом "выбросов", имеющих принципиально иное распределение. Как считает А.И. Орлов [22] эта модель представляется "тупиковой", поскольку в большинстве случаев большие выбросы либо невозможны из-за ограниченности шкалы прибора, либо от них можно избавиться, применяя лишь статистики, построенные по центральной части вариационного ряда.
Перспективной представляется модель Ю.Н. Благовещенского [3], в которой расстояние между распределением каждого элемента выборки и базовым распределением не превосходит заданной малой величины.
Размножение выборок (бутстреп)
Основная идея бутстрепа реализуется таким образом, чтобы теоретическое исследование заменить вычислительным экспериментом. Вместо описания выборки распределением из параметрического семейства требуется построить большое число "похожих" выборок, т.е. "размножить" выборку. Затем вместо оценивания характеристик и параметров, и проверки гипотез на основе свойств теоретического распределения решаются эти задачи вычислительным методом, рассчитываются статистики по каждой из "похожих" выборок и анализируются полученные при этом распределения.
Преимущества и недостатки бутстрепа как статистического метода обсуждаются А.И. Орловым [17, 18]. В указанных работах приводится информация о ряде аналогичных методов. При этом следует отметить, что бутстреп по Б. Эфрону [34, 35] - лишь один из вариантов методов "размножения выборки", и, как считает А.И. Орлов [22, не самый удачный. Этому автору метод "складного ножа" представляется более полезным. На его основе он сформулировал следующую простую практическую рекомендацию - можно изменять не выборку, а сами данные.
В связи с тем, что в измерениях всегда имеются погрешности, то реальные данные - это не числа, а интервалы (результат измерения плюс-минус погрешность).
Статистика интервальных данных
Перспективное и в последние годы быстро развивающееся направление последних лет - математическая статистика интервальных данных. Речь идет о развитии методов математической статистики в ситуации, когда статистические данные - интервалы, в частности, порожденные наложением ошибок измерения на значения случайных величин.
Статистика интервальных данных связана с интервальной математикой, в которой в роли чисел выступают интервалы [32]. Это направление математики является дальнейшим развитием правил приближенных вычислений, посвященных выражению погрешностей суммы, разности, произведения, частного через погрешности тех чисел, над которыми осуществляются перечисленные операции. Как следует из сообщений, представленных на Международной конференции по интервалам и стохастическим методам в науке и технике [25], уже удалось решить некоторые задачи теории интервальных дифференциальных уравнений, в которых для описания и решения используются интервалы, коэффициенты, начальные условия и решения.
Возглавляет это научной направление в области статистики интервальных данных - школа проф. А.П. Вощинина. Результаты работы этой школы представлены в ряде монографий [5 - 7 и др.].
Согласно классификации статистических методов, принятой в 1987 году [24], прикладная статистика делится на следующие четыре области:
- статистика (числовых) случайных величин,
- многомерный статистический анализ,
- статистика временных рядов и случайных процессов,
- статистика объектов нечисловой природы.
Первые три области классические. Четвертая - только входит в массовое сознание специалистов. Ее называют статистикой нечисловых данных или нечисловой статистикой.
Статистика объектов нечисловой природы
Исходным объектом в статистике является выборка. В вероятностной теории статистики выборка представляет собой совокупность независимых одинаково распределенных случайных элементов. Какова же природа таких элементов? В классической статистике элементы выборки - это числа. В многомерном статистическом анализе - вектора. А в нечисловой статистике элементы выборки - это объекты нечисловой природы, которые нельзя складывать и умножать на числа. Таким образом, объекты нечисловой природы лежат в пространствах, не имеющих векторной структуры.
Примерами объектов нечисловой природы являются:
1) значения качественных признаков, т.е. результаты кодировки объектов с помощью заданного перечня категорий (градаций);
2) упорядочения (ранжировки) экспертами образцов продукции или заявок на проведение научных работ (при проведении конкурсов на выделение грантов);
3) классификации, т.е. разбиения объектов на группы сходных между собой признаков (кластеры);
4) толерантности, т.е. бинарные отношения, описывающие сходство объектов между собой, например, сходства тематики научных работ, оцениваемого экспертами с целью рационального формирования экспертных советов внутри определенной области науки;
5) результаты парных сравнений или контроля качества продукции по альтернативному признаку ("годен" - "брак"), т.е. последовательности из 0 и 1;
6) множества (обычные или нечеткие), например, зоны, пораженные коррозией, или перечни возможных причин аварии, составленные экспертами независимо друг от друга;
7) слова, предложения, тексты;
8) вектора, координаты которых - совокупность значений разнотипных признаков, например, результат составления статистического отчета о научно-технической деятельности или заполненная компьютеризированная история болезни, план подготовки спортсмена, в которой часть признаков носит качественный характер, а часть - количественный;
9) ответы на вопросы экспертной, маркетинговой или социологической анкеты, часть из которых носит количественный характер (возможно, интервальный), часть сводится к выбору одной из нескольких подсказок, а часть представляет собой тексты; и т.д.
Интервальные данные тоже можно рассматривать как пример объектов нечисловой природы, как частный случай нечетких множеств.
Как отмечает А.И. Орлов [22] к 90-м годам статистика объектов нечисловой природы с теоретической точки зрения была достаточно хорошо развита. Однако она оставалась весьма слабо использованной для практических потребностей. В 90-е годы началось интенсивное применение полученных математико-статистических исследований в практической сфере.
Следует отметить, что в статистике объектов нечисловой природы, как и в других областях прикладной математической статистики и прикладной математики вообще, одна и та же математическая схема может с успехом применяться и в технических исследованиях, медицине, социологии, физической культуре и спорте высших достижений, и для анализа экспертных оценок.
Для анализа нечисловых, например, экспертных данных, весьма важны методы классификации. Между тем, наиболее естественно ставить и решать задачи классификации, основанные на использовании расстояний или показателей различия, в рамках статистики объектов нечисловой природы. Это касается как распознавания образов с учителем (другими словами, дискриминантного анализа), так и распознавания образов без учителя (т.е. кластерного анализа). Современное состояние дискриминантного и кластерного анализа с точки зрения статистики объектов нечисловой природы представлено работе А.И. Орлова [21].
В работе показаны пять перспективных "точек роста" прикладной статистики как методической дисциплины. Эти "точки" не исчерпывают разнообразие направлений научных исследований в этой области. Много интересных проблем есть в планировании экспериментов, особенно кинетических [9], при анализе проблем надежности [28], в новых статистических методах управления качеством продукции, в том числе в связи с идеями Г. Тагути [1] и др.
Анализ временных рядов
В настоящее время одним из методов статистического анализа при обработке разнообразных данных о человеке, который позволяет делать достаточно тонкие исследования является анализ временных серий или анализ временных рядов (ВР). Эти ряды представляют собой упорядоченную во времени совокупность наблюдений случайной величины или процесса, т.е. это ряд (или серия) чисел, каждое из которых задает значение наблюдаемой случайной величины в определенный момент времени. Как правило, моменты времени являются равноотстоящими друг от друга. Такими равноотстоящими моментами времени могут быть часы, дни, месяцы, годы и т.д.
Упорядоченность элементов ряда является важным свойством такой совокупности наблюдений и это обстоятельство отличает его от простого набора значений случайной величины и позволяет получить дополнительны и весьма ценные результаты.
Вопросы анализа временных рядов (ВР) относятся к числу наиболее интересных и важных с точки зрения их прикладного использования. Особенно в спорте, когда возникают задачи оценки состояния подготовленности спортсменов и его прогнозирования у отдельно взятых спортсменов.
Задача анализа ВР состоит в преобразовании одномерного ряда первичных данных в многомерный. При этом возможно выделение отдельных слагаемых первичного ряда - медленную тенденцию (тренд), сезонные колебания, возможные периодические составляющие и случайные отклонения. Это, в свою очередь, позволяет прогнозировать как сам ВР, так и тенденции развития различных его составляющих.
Далее будут представлены методы анализа ВР.
В отличие от анализа случайных выборок, анализ ВР основывается на предположении, что последовательные значения в файле данных наблюдаются через равноотстоящие интервалы времени.
Детальное представление указанных методов подано в работах: [4, 36, 37, 39 - 41 и др.].
Основные цели анализа ВР рядов - это определение природы ряда и прогнозирование.
В первую очередь при анализе ВР ряда необходимо выделить систематическую составляющую и случайный шум.
Анализ ВР предполагает, что первичные данные содержат систематическую составляющую (состоящую из одной или несколько компонент) и случайный шум (ошибку), усложняющую обнаружение других компонент.
Большинство регулярных составляющих ВР принадлежит к двум классам - они являются либо трендом, либо сезонной составляющей. Тренд представляет собой общую систематическую линейную или нелинейную компоненту, которая может изменяться во времени. Сезонная составляющая - это периодически повторяющаяся компонента. Оба эти вида регулярных компонент часто присутствуют в ряде одновременно.
Не существует "автоматического" способа обнаружения тренда в ВР. Однако если тренд является монотонным (устойчиво возрастает или устойчиво убывает), то анализировать такой ряд обычно нетрудно. Если временные ряды содержат значительную ошибку, то первым шагом выделения тренда является их сглаживание.
Сглаживание всегда включает некоторый способ локального усреднения данных, при котором несистематические компоненты взаимно погашают друг друга. Самый общий метод сглаживания - скользящее среднее, в котором каждый член ряда заменяется простым или взвешенным средним n соседних членов, где n - ширина "окна" [см. 4].
Когда ошибка измерения очень большая обычно применяется один из методов сглаживания - метод наименьших квадратов, взвешенных относительно расстояния или метод отрицательного экспоненциально взвешенного сглаживания. Перечисленные методы фильтруют случайные воздействия и преобразуют данные в относительно гладкую кривую.
Периодическая и сезонная зависимости являются другими общими типами компонент ВР. В общем, периодическая зависимость может быть формально определена как корреляционная зависимость порядка k между каждым i-м элементом ряда и (i-k)-м элементом [12]. Ее можно измерить с помощью автокорреляции (т.е. корреляции между самими членами ряда).
Сезонные составляющие компоненты ВР могут быть найдены с помощью корреляционных методов. Коррелограмма (автокоррелограмма) показывает численно и графически автокорреляционную функцию.
При анализе коррелограмм следует помнить, что автокорреляции последовательных шагов формально зависимы между собой. Это приводит к тому, что периодическая зависимость может существенно измениться после удаления автокорреляций первого порядка.
Периодическая составляющая для данного k может быть удалена взятием разности соответствующего порядка. Это означает, что из каждого i-го элемента ряда вычитается (i-k)-й элемент. Используются два довода в пользу таких преобразований:
1) таким образом можно определить скрытые периодические составляющие ряда,
2) удаление сезонных составляющих делает ряд стационарным.
Для иллюстрации приведем результаты исследования группы спортменов в течение 100 дней ежедневно. В связи с тем, что авторами были проведены лонгитуденальные исследования, изучаемых физиологических показателей использовалась батарея статистических методов, используемых для анализа временных рядов (ВР). В таких рядах данных и особенно в биологических объектах исследований наблюдения зависимы и характер этих зависимостей представляет самостоятельный теоретический и практический интерес.
Известно, что многочисленные исследования ВР [12, 15, 27] показали, что такие данные в конечном итоге представляют собой алгебраическую сумму следующих компонентов:
1. систематического движения исследуемого процесса во времени (тренда),2. колебаний состояния относительно тренда с большей или меньшей регулярностью,
3. эффекта "сезонности",
4. "случайной", "несистематической" или "нерегулярной" составляющей.
Анализ таких рядов предполагает такую процедуру, которая сводится к разложению ВР на все перечисленные компоненты, а затем каждая из них последовательно изучается [12, 33].
На примере ВР, получено при исследовании исп. Б - ва продемонстрируем систему анализа полученных нами данных.
Шаг 1. На рис. 1. представлена динамика воспроизведения заданного усилия (ВЗУ) (50 % от максимального), выраженного в килограммах. Как видно из представленных данных ВР не является линейной функцией времени, а представляет собой колебательный процесс, напоминающий запись "белого шума". Однако при внимательном рассмотрении графика в колебаниях состояния проприоцептивной сенсорной системы можно отметить минимумы и максимумы ВЗУ, имеющих нерегулярный характер.
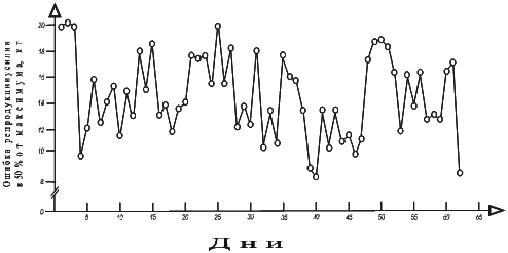
Рис. 1. Динамика воспроизведения заданного усилия в 50 % от максимального (кг)
Шаг 2. На рис. 2 представлен конечный результат (фильтрации) следующего шага статистического анализа - расчета линии тренда с помощью линейной интерполяции кусочно-линейными функциями. И как видно из представленных данных тренд также во времени является нерегулярной функцией. Он представляет собой сложное долговременное апериодическое колебание.
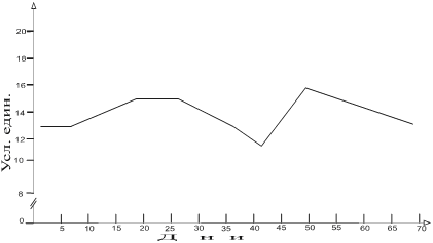
Рис. 2. Динамика линии тренда воспроизведения заданногоусилия (50 % от максимального, кг)
Шаг 3. Дале проводится исключение из первичного ряда апериодического тренда. Результат этого шага представлен на рис. 3. В приведенных на рисунке "остаточных" (отфильтрованных) данных остались еще два компонента ВР - неизвестный колебательный процесс и случайная компонента. Для того, чтобы получить ответ о наличии (или отсутствии) и параметрах неизвестного колебательного процесса эту случайную компоненту необходимо элиминировать.
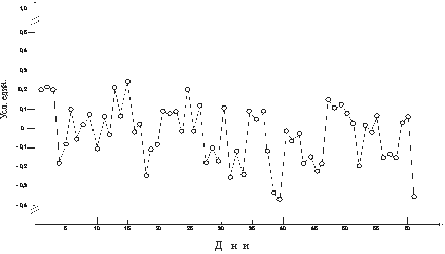
Рис. 3. "Остаточные" данные динамики воспроизведения заданного усилия (50 % от максимального, кг)
Шаг 4. Как отмечалось выше произвести операцию элиминирования "случайной" компоненты можно различными методами. И выполнение такого шага обусловлено тем, что существует так называемый "феномен Слуцкого-Юла" [26]. Сущность этого явления связана с тем, что при использовании некоторых методов (фильтрования) статистического анализа ВР с целью элиминации случайной компоненты в эти ряды искусственно вносится элемент периодической компоненты. Не вдаваясь в тонкие детали этого метода [11], мы отметим, что применение одного из наиболее простых и доступных статистических методов элиминации случайных составляющих ВР - метода скользящего сглаживания, может привести к ошибочным заключениям.
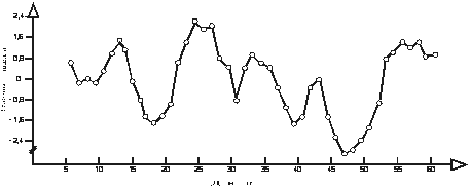
Рис. 4. Скользящее сглаживание по 5-ти точкам "остаточных" данных динамики воспроизведения заданного усилия (50 % от максимального, кг)
Как видно из представленных на рис. 4 данных в изучаемом процессе присутствует скрытая периодическая компонента с четко выраженными фазами повышения и понижения функционального состояния двигательной сенсорной системы при оценке заданного мышечного усилия. Наблюдаемый процесс не является строго периодическим, а относится к числу так называемых колебаний квазипериодического типа. Однако, зная возможности метода скользящего сглаживания привносить периодическую компоненту, мы ставим под сомнение полученные результаты, поскольку они могут быть результатом проявления "феномена Слуцкого-Юла". Чтобы убедиться в истинности полученных данных, очевидно, необходимо применить какие-то иные методы анализа, имеющие независимые между собой и методом скользящего сглаживания правила вычислений.
Шаг 5. Для указанных целей было использовано два метода - метод автокорреляционной функции и периодограмманализа.
Как видно из представленного на рис. 5 результатов вычисления автокорреляционной функции в изучаемом процессе подтверждается наличие периодической компоненты. Таким образом, в динамике функционального состояния двигательной сенсорной системы квазипериодические колебания не являются артефактом, т. к. они сохраняются и при использовании принципиально другого метода выявления скрытых периодических компонентов ВР.
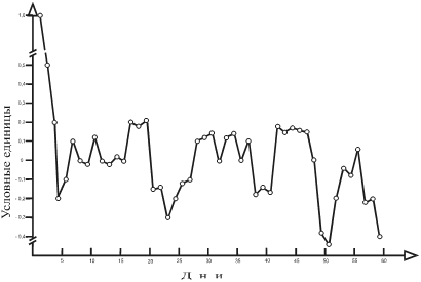
Рис. 5. Автокорреляционная функция динамики воспроизведения заданного усилия (50 % от максимального, кг)
Но, к сожалению, метод автокорреляции не дает возможности однозначно определить продолжительность доминирующего или других периодов колебаний.
Шаг 6. Указанный выше недостаток позволяет исключить другой метод анализа - периодограмманализ (рис. 6).
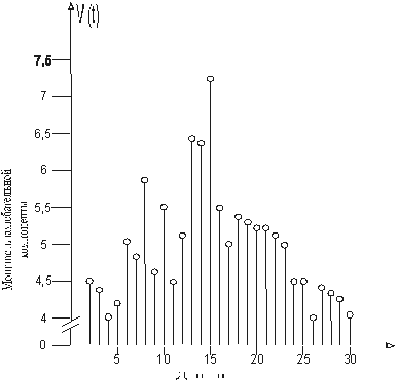
Рис. 6. Периодограмма динамики воспроизведения заданногоусилия (50 % от максимального, кг)
Таким образом, комплекс непараметрических методов статистического анализа первичных данных позволяет утверждать, что во времени состояние двигательной сенсорной системы при воспроизведении заданного усилия скелетных мышц спортсмена (50 % от максимального, кг) не является постоянной величиной, а носит колебательный характер. Эти колебания характеризуются наличием наряду с суточными, сезонными и квазипериодических колебаний с периодом в 10-12 дней.
Такой результат подтвердили разнообразные статистические методы анализа.
В работе показана последовательность обработки первичных данных для индивидуального анализа функционального состояния организма спортсменов и динамики их спортивных показателей, которые можно при современном состоянии информатики и вычислительной техники использовать с высокой степенью эффективности для диагностики и прогнозирования всех структурных элементов тренировочного процесса и сделать его более гибким, индивидуальным и быстрым.
Обобщая, можно сказать, что использование метода временных рядов возможно в любых исследованиях, где наблюдения проводятся через равноотстоящие промежутки времени.
Следующие шаги, с помощью которых можно прогнозировать динамику квазипериодического процесса, - это уже тема иной работы авторов.
Литература
1. Адлер Ю.П., Талалай А.М. (1992) Курс на качество. № 3 - 4. С. 85-93.
2. Бернштейн С.Н. (1928) В сб.: Труды Всероссийского съезда математиков в Москве 27 апреля - 4 мая 1927 г. - М.-Л.: ГИЗ.- С.50-63.
3. Благовещенский Ю.Н. (1973) В сб.: Тезисы докладов Международной конференции по теории вероятностей и математической статистике. Вильнюс, 25-30 июня 1973 г. Т.1. - Вильнюс: Изд-во Вильнюсского госуниверситета. - С.77-78.
4. Бокс Дж., Дженкинс Г. (1974) Анализ временных рядов. Прогноз и управление (Вып. 1, 2). М., Мир.
5. Вощинин А.П. (1987) Метод оптимизации объектов по интервальным моделям целевой функции. - М.: МЭИ.
6. Вощинин А.П., Сотиров Г.Р. (1989) Оптимизация в условиях неопределенности. - М.: МЭИ - София: Техника.
7. Вощинин А.П., Акматбеков Р.А. (1991) Оптимизация по регрессионным моделям и планирование эксперимента. - Бишкек: Илим.
8. Гнеденко Б.В., Орлов А.И. (1988) Заводская лаборатория. - Т.54. № 1. С. 1-4.
9. Горский В.Г. (1997) В сб.: Международная школа повышения квалификации "Инженерно-химическая наука для передовых технологий". Труды третьей сессии, 26-30 мая 1997. Казань, Россия /Под ред. В.А. Махлина. - М.: Научно-исследовательский Физико-химический Институт им. Карпова. С.261-293.
10. Гуда А.Н. (1997) Модели, методы и средства анализа данных в затрудненных условиях. Автореф. дисс. докт. технич. наук. - Таганрог: Таганрогский государственный радиотехнический университет.
11. Иванов К.П. Биоэнергетика и температурный гомеостаз. - Л.: Наука, 1972. - 172 с.
12. Кендал М.Дж., Стьюарт А. (1976) Многомерный статистический анализ и временные ряды. - М.: Наука.
13. Клейн Ф. (1937) Лекции о развитии математики в 19 столетии. Часть I. - М. -Л.: Объединенное научно-техническое издательство НКТП СССР.
14. Комаров Д.М., Орлов А.И. (1988) В сб.: Вопросы применения экспертных систем. - Минск: Центросистем, - С. 151-160.
15. Курский М.Д., Бакшеев Н.С. (1974) Биохимические основы механизма действия серотонина. - Киев, Наукова думка.
16. Налимов В.В. (1994) Канатоходец. Воспоминания. - М.: Издательская группа "Прогресс".
17. Орлов А.И. (1987) Надежность и контроль качества. - № 6. - С. 54-59.
18. Орлов А.И. (1987) Заводская лаборатория. Т. 53. № 10. - С. 82-85.
19. Орлов А.И. (1991) Заводская лаборатория. Т. 57. № 7. - С. 64-66.
20. Орлов А.И. (1991) Надежность и контроль качества. № 8. - С. 3-8.
21. Орлов А.И. (1992) Социология: методология, методы, математические модели. № 2. - С. 28-50.
22. Орлов А.И. (1995) Заводская лаборатория. Т. 61. № 7. -С. - 59-61.
23. Орлов А.И. (2004) http://www.nickart.spb.ru/analysis/text_07.php
24. Прикладная статистика. (1987) Методы обработки данных. Основные требования и характеристики. - М.: ВНИИСтандартизации,. - 64 с.
25. Сборник трудов Международной конференции по интервальным и стохастическим методам в науке и технике. (1992) Т. 1, 2. - М.: МЭИ.
26. Слуцкий Е.Е. Сложение случайных причин как источник циклический процессов. "Вопросы конъюнктуры", 1927. т. 3. - С. 34-65.
27. Стырыкович В.Л. (1940) Анализ весовых кривых в грудном возрасте. (Применительно к вскармливанию). - Л.
28. Тескин О.И. (1995) В сб.: Статистические методы оценивания и проверки гипотез. Межвузовский сборник научных трудов. - Пермь: Изд-во Пермского государственного университета. - С. 227 - 236.
29. Управление большими системами. Материалы международной научно-практической конференции (22-26 сентября 1997 г., Москва, Россия). (1997) Общая редакция - Бурков В.Н., Новиков Д.А. - М.: СИНТЕГ.
30. Хампель Ф., Рончетти Э., Рауссеу П., Штаэль В. (1989) Робастность в статистике. Подход на основе функций влияния. - М.: Мир.
31. Холландер М., Вулф Д. (1985) Непараметрические методы статистики. - М.: Финансы и статистика.
32. Хьюбер П. (1984) Робастность в статистике. - М.: Мир.
33. Шокин Ю.И. (1992) Эволюционное моделирование и кинетика. Новосибирск, Наука.
34. Энтов Р.М., Дробышевский С.М., Носко А.Д. (2001) Экономический анализ динамических рядов основных макроэкономических показателей. М.
35. Эфрон Б. (1988) Нетрадиционные методы многомерного статистического анализа. - М.: Финансы и статистика,.
36. Efron B. (1979) Ann. Statist. V.7. № 1. - P.1-26.
37. Kaczmarek M. (2001) Poznańskie Badania Longitudinalne. Rozwój fizyczny chłopców i dziewcząt. Monografia Instytutu Antropologii UAM9.
38. Kendall M.G. (1952) The Advanced Theory of Statistics, t. 1, wyd. 5, London, Charles Griffin and Co.
39. Kendall M.G., Stuart A., Keith J. 1977-(1983) The Advanced Theory of Statistics, t. 1-3, wyd. 4, London, Charles Griffin and Co.
40. Kościński K. (2003) Wyznaczenia zakresu normy - podejście statystyczne i empiryczne. Metody statystyczne w antropologii. AWF J. Piłsudskiego, Warszawa. - S. 49-60.
41. Kozieł S. (2003) Metodologiczne aspekty analizy danych longitudinalnych na przykładzie modeli strukturalnych Preece-Bainsa i Jensa-Bayley’a. Metody statystyczne w antropologii. AWF J. Piłsudskiego, Warszawa. - S. 89-100.
42. Sokal R.R., Rohlt E.J. (1995) Biometry. The principles and practice of statistics of biological research. N.-Y., W.H. Freeman and Company.
Поступила в редакцию 25.05.2004г