АНАЛИЗ ИНФОРМАТИВНОСТИ СТЕПЕНИ ИСПОЛЬЗОВАНИЯ СИЛОВЫХ ВОЗМОЖНОСТЕЙ ПРИ ОТТАЛКИВАНИИ В СОЧЕТАНИИ С ВОЗРАСТОМ, ВЕСОМ И РОСТОМ ПРЫГУНОВ В ВЫСОТУ В ЗАДАЧАХ ПРОГНОЗА ИХ РЕЗУЛЬТАТИВНОСТИ
Ахметов Р.Ф.
Житомирский государственный университет имени Ивана Франко
Аннотация. Рассматривается задача прогноза результативности прыгунов в высоту, используя важнейший параметр спортсменов - степень использования силовых возможностей при отталкивании в сочетании с антропометрическими параметрами (рост, вес) и возрастом спортсменов.
Ключевые слова: аппроксимация, регрессионная матрица, линейная регрессия.
Анотацiя. Ахметов Р.Ф. Аналiз iнформативностi ступеня використання силових можливостей при вiдштовхуваннi в поеднаннi з вiком, вагою та зростом стрибунiв у висоту в задачах прогнозу iх результативностi. Розглядаеться задача прогнозу результативностi стрибунiв у висоту, використання найважливiший параметр спортсменiв - ступiнь використовування силових можливостей при вiдштовхуваннi в поеднаннi з антропометричними параметрами (зрiст, вага) та вiком спортсменiв.
Ключовi слова: апроксимацiя, регресiйна матриця, лiнiйна регресiя.
Annotation. Akhmetow R.F. Analytical treatment of the degree of employing the spring-off force along with age, weight and height characteristics intended for high jump efficiency estimate. The paper addresses the problem of high-jump efficiency estimale by means of the degree of employing the spring force along with age, weight and height characteristics of athlets as a most important athletic parameter.
Key words: approximation, regression matrix, linear regression.
Постановка проблемы. В работе [3] была исследована информативность параметров - степени использования силовых возможностей при отталкивании и возраста прыгунов в высоту в задаче одномерного прогноза их результативности (в смысле раздельного решения задач одномерной линейной регрессии [1; 2] для каждого из параметров). При этом, однако, отмечая более высокую информативность степени использования силовых возможностей при отталкивании (СВТ) по отношению к возрасту, в работе [3] не был рассмотрен вопрос о совместной (двумерной) информативности обоих параметров, как решение задачи двумерной линейной регрессии. Последняя задача решается в данной работе на базе общей теории прогноза результативности спортсменов [2; 4; 5]. При этом возраст формально включается в полную совокупность спортивных параметров под номером 5 (для простоты в совокупности из 21 параметра [1] малоинформативный параметр - 5 (длина бедра) - заменяется возрастом 10-17 лет). Кроме того, в данной работе рассматриваются также вопросы повышения информативности СВТ в сочетании с двумя антропометрическими параметрами - вес и рост.
Анализ последних исследований и публикаций. Как показано в работе [3], одновременный удовлетворительный прогноз на период до 17 лет по СВТ и возрасту можно сделать на базе данных в период 10-14 лет (среднеквадратическое отклонение (СКО) прогноза менее 4 см). Задачу прогноза результативности спортсменов [1; 2; 4; 5] можно решать на базе факторного анализа и динамики развития физических параметров и результатов на некотором ограниченном интервале времени (например, 10-13-14 лет). В данной работе даются приложения общего подхода [2; 5] к частной задаче прогноза результативности прыгунов в высоту при использовании различных одномерных, двумерных, трехмерных и четырехмерной комбинаций спортивных параметров из четырехмерной совокупности.
Работа проводилась по теме 1.4.7 "Совершенствование технического мастерства легкоатлетов-прыгунов в процессе их многолетней подготовки" согласно плана научно-исследовательских работ Госкомспорта Украины на 2001-2005 гг. Номер госрегистрации: 0101U006316.
Целью настоящего исследования была разработка программы прогнозирования результативности прыгунов в высоту на базе таких важных параметров, как степень использования силовых возможностей при отталкивании (СВТ), возраст, вес и рост спортсменов.
Результаты исследования. Для анализа была выбрана одна группа из 12 спортсменов [1; 2] и прослежена динамика роста результативности (высоты прыжка Н) в зависимости от спортивных параметров по 8 возрастным периодам (t = 10-17 лет). Расширенный перечень параметров спортсменов представляется в виде:
- Спортивный результат (высота) - Целевая функция.
- Рост.
- Длина голени.
- Длина бедра.
- Окружность бедра (в данной работе заменяется в расчетах на возраст).
- Окружность икроножной мышцы.
- Вес.
- Скорость разбега перед отталкиванием.
- Скорость вылета ОЦТ (в момент отрыва).
- Угол вылета ОЦТ.
- Длительность фазы отталкивания.
- Высота вылета ОЦТ.
- Импульс силы отталкивания.
- Степень использования силовых возможностей толчка (%).
- Бег - 30 м (с).
- Скорость спринтерского бега (10 м с хода).
- Прыжок вверх в высоту с двух ног с места.
- Прыжок в длину с места.
- Тройной прыжок с места.
- Прыжок вверх с толчковой ноги (махом другой).
- Прыжок вверх в высоту с трех шагов.
АНТРОПОМЕТРИЧЕСКИЕ ПАРАМЕТРЫ (2-7)
ТЕХНИЧЕСКИЕ ПАРАМЕТРЫ (8-14)
(Регистрируемые и расчетные показатели технической подготовки)
СПЕЦИАЛИЗИРОВАННЫЕ ПАРАМЕТРЫ (15-21)
(Уровень специальной физической подготовки)
Поскольку результаты и физические параметры спортсменов в группе имеют случайный разброс (дисперсию), то, говоря о задаче прогноза результативности, имеет смысл рассматривать прогноз средней результативности
![]() , как функции средних по группе физических параметров
, как функции средних по группе физических параметров
![]() , которые будем представлять в виде матрицы столбца:
, которые будем представлять в виде матрицы столбца:
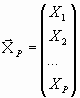 , P=1,2,...,N1-1; N1>2,
, P=1,2,...,N1-1; N1>2,
где N1 - полное число спортивных параметров, включая сам результат (Н). Полное множество Р-мерных группировок из (N1-1) по Р равно числу сочетаний из (N1-1) по Р:
![]()
![]() , (1)
, (1)
![]() .
.
В данной работе N1=21, Р=1,2,3,4:
X1 = x5 (время), X2 = x14 (СВТ), X3 = x7 (вес), X4 = x2 (рост),
K = C14 + C24 + C34 + C44 = 4 + 6 + 4 + 1 = 15
где К=15 - общее количество различных комбинаций информативных параметров.
Информативность различных Р-мерных группировок
![]() в задачах прогноза результативности будет также различной. Вопрос о выборе оптимальной совокупности наиболее информативных параметров из множества (1) при различных Р требует самостоятельных глубоких исследований в рамках отдельной НИР. В данной работе предлагается один из альтернативных вариантов решения задачи, который вполне приемлем с точки зрения точности прогноза. В первом приближении рассматривается задача линейного прогноза в рамках классической теории линейной регрессии (интерполяции) в математической статистике. Речь идет о нахождении аппроксимации
в задачах прогноза результативности будет также различной. Вопрос о выборе оптимальной совокупности наиболее информативных параметров из множества (1) при различных Р требует самостоятельных глубоких исследований в рамках отдельной НИР. В данной работе предлагается один из альтернативных вариантов решения задачи, который вполне приемлем с точки зрения точности прогноза. В первом приближении рассматривается задача линейного прогноза в рамках классической теории линейной регрессии (интерполяции) в математической статистике. Речь идет о нахождении аппроксимации
![]() , (2)
, (2)
где ![]() - неизвестные параметры регрессии, которые требуется оценить по данным некоторого количества возрастных групп. В более точной постановке приближенная линейная регрессия (2) представляется в виде:
- неизвестные параметры регрессии, которые требуется оценить по данным некоторого количества возрастных групп. В более точной постановке приближенная линейная регрессия (2) представляется в виде:
![]() , (3)
, (3)
где ![]() - ошибка прогноза с нулевым средним (
- ошибка прогноза с нулевым средним (![]() ) и неизвестной дисперсией
) и неизвестной дисперсией
![]() (M - оператор математического ожидания - среднего). Если в результате решения задачи линейной регрессии на интервале времени
T получены оценки неизвестных параметров регрессии:
(M - оператор математического ожидания - среднего). Если в результате решения задачи линейной регрессии на интервале времени
T получены оценки неизвестных параметров регрессии:
![]()
то прогнозное значение средней результативности вне этого интервала представляется в виде:
![]() (4)
(4)
где набор физических параметров {![]() } - задается на прогнозируемый момент времени to. При этом среднеквадратическая ошибка (СКО) прогноза оценивается величиной
} - задается на прогнозируемый момент времени to. При этом среднеквадратическая ошибка (СКО) прогноза оценивается величиной
![]() Насколько "удачно" получена оценка (4), - зависит от многих факторов и последнее слово здесь за практикой (экспериментальной апробации). Проведенная в данной работе апробация модели (4) показывает, что она практически вполне приемлема. СКО при этом не превышает 4.6 сантиметров и минимум СКО=3,1 см достигается для одномерного параметра - СВТ для прогноза на период до 17 лет включительно. Отметим, что формальное включение возраста в число физических параметров спортсменов может привести, вообще говоря, к потери эффективности прогноза результативности, особенно для многомерных сочетаний параметров. Это связано с квазилинейной зависимостью большинства истинных физических параметров от времени (возраста). Экспериментальные исследования, проведенные в данной работе, подтверждают указанную особенность: для 4-х мерной совокупности (СВТ, возраст, вес, рост) оказывается, что СКО прогноза до 17 лет не уменьшается, а возрастает до недопустимых величин (более 10 см).
Насколько "удачно" получена оценка (4), - зависит от многих факторов и последнее слово здесь за практикой (экспериментальной апробации). Проведенная в данной работе апробация модели (4) показывает, что она практически вполне приемлема. СКО при этом не превышает 4.6 сантиметров и минимум СКО=3,1 см достигается для одномерного параметра - СВТ для прогноза на период до 17 лет включительно. Отметим, что формальное включение возраста в число физических параметров спортсменов может привести, вообще говоря, к потери эффективности прогноза результативности, особенно для многомерных сочетаний параметров. Это связано с квазилинейной зависимостью большинства истинных физических параметров от времени (возраста). Экспериментальные исследования, проведенные в данной работе, подтверждают указанную особенность: для 4-х мерной совокупности (СВТ, возраст, вес, рост) оказывается, что СКО прогноза до 17 лет не уменьшается, а возрастает до недопустимых величин (более 10 см).
Матричное решение задачи линейной регрессии результативности по заданной совокупности наиболее информативных параметров.
Для оценки параметров регрессии
![]() составляется следующая система линейных алгебраических уравнений:
составляется следующая система линейных алгебраических уравнений:
![]()
![]() (5)
(5)
.....................................
![]() ,
,
где в данном разделе, следуя стандартным обозначениям, N - число возрастных групп (в данной работе N<9). Система (5) представляется в матричном виде:
![]() (6)
(6)
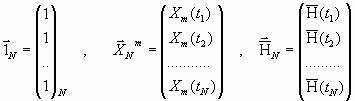 .
.
Вводя т.н. "сигнальный" регрессионный вектор (СРВ):
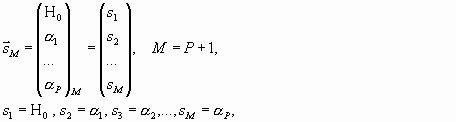 (7)
(7)
матричную систему (6) представляем также в стандартном виде:
![]() (8)
(8)
![]()
где ![]() - измеримая матрица наблюдений (ИМН);
- измеримая матрица наблюдений (ИМН); ![]() - измеримый вектор средних результатов (ВСР).
- измеримый вектор средних результатов (ВСР).
Согласно общей теории линейной регрессии система (8) может быть решена, если она полностью определена или переопределена:
![]() . (9)
. (9)
Отметим, что величина (М+1) обусловлена тем, что в число неизвестных помимо М=Р+1 неизвестных параметров регрессии необходимо включить также и неизвестное СКО
![]() . При выполнения условия (9) статистическое решение задачи линейной регрессии представляется в виде:
. При выполнения условия (9) статистическое решение задачи линейной регрессии представляется в виде:
![]() , (10)
, (10)
![]() , (11)
, (11)
![]() ,
,
![]() ,
,
где ![]() - псевдообратная матрица;
- псевдообратная матрица; ![]() - проектор в линейную оболочку из базисных векторов {
- проектор в линейную оболочку из базисных векторов {![]() };
}; ![]() - ортогональный проектор.
- ортогональный проектор.
Специфической математической особенностью задачи регрессии спортивного результата является то, что в силу довольно однородного состава групп столбцовые вектора ИМН
![]() оказываются хотя и случайными, но с малым угловым расхождением относительно "единичного" вектора
оказываются хотя и случайными, но с малым угловым расхождением относительно "единичного" вектора
![]() . Последнее обстоятельство требует жесткого контроля точности обращения матрицы Грама
. Последнее обстоятельство требует жесткого контроля точности обращения матрицы Грама
![]() , т.к. в случае высокой угловой корреляции ("схожести") векторов
, т.к. в случае высокой угловой корреляции ("схожести") векторов
![]() матрица Грама оказывается часто плохо обусловленной с большим динамическим диапазоном собственных чисел в области малых величин. При этом точность обращения матрицы Грама с ростом размерности Р>3 (числа учитываемых информативных параметров) начинает резко падать и дальнейшее увеличение размерности Р не представляется возможным, - что подтверждается экспериментально в данной работе для Р=4.
матрица Грама оказывается часто плохо обусловленной с большим динамическим диапазоном собственных чисел в области малых величин. При этом точность обращения матрицы Грама с ростом размерности Р>3 (числа учитываемых информативных параметров) начинает резко падать и дальнейшее увеличение размерности Р не представляется возможным, - что подтверждается экспериментально в данной работе для Р=4.
Отметим также, что в данной работе максимальное число возрастных групп Nmax=8. Поэтому в силу условия (9) предельное число наиболее информативных параметров ограничивается величиной 6:
![]() .
.
Разработана специализированная программа cor2d.com (модификация программы corrS2m.com) в среде Turbo Pascal, которая содержит следующие пункты:
1. Вызов исходных статистических данных ( файл g1_21_9.dat ).2. Шифр файла: ТN(21)-M(
, где N - число возрастных групп, по которым проводится прогноз на будущее; М - число информативных параметров (N>M+2).
3. Выбор М информативных параметров ( из номеров 2-21 [1]).
4. Анализ ранга регрессионной матрицы
методом Грама-Шмидта.
5. Анализ корреляции информативных параметров по годам.
6. Спектральный анализ матрицы Грама
размером (М+1)*(М+1).
7. Оценка точности обращения матрицы Грама.
8. Оценка статистических характеристик информативных параметров (средние, СКО, корреляционная матрица).
9. Решение задачи линейной регрессии.
10. Оценка дисперсии шума (СКО=s).
11. Прогнозирование за пределы выбранных возрастных групп на период до 17 лет.
Далее приводятся только графики по пункту 11 зависимости оценки средней результативности (4) от времени t (возраста), которая называется оперативной динамической характеристикой результативности (ОДХР).
Экспериментальные исследования эффективности прогноза результативности
Исходные данные по 21 параметру (5-годы) для 8 возрастных групп 10-17 лет взяты из [1]:
1=> 1.17 1.38 1.52 1.62 1.72 1.87 1.94 2.01
2=> 1.49 1.54 1.59 1.65 1.70 1.77 1.84 1.89
3=> 0.34 0.35 0.36 0.37 0.38 0.39 0.40 0.41
4=> 0.35 0.36 0.37 0.38 0.39 0.40 0.41 0.42
5=> 10.00 11.00 12.00 13.00 14.00 15.00 16.00 17.00
6=> 0.27 0.28 0.29 0.30 0.31 0.32 0.33 0.35
7=> 38.13 43.46 48.37 53.83 59.38 65.83 71.29 77.42
8=> 4.39 4.81 5.15 5.41 5.63 5.87 6.07 6.32
9=> 3.02 3.51 3.71 3.92 4.09 4.39 4.57 4.76
10=> 48.92 50.03 50.42 51.01 51.37 52.46 52.70 52.94
11=> 0.27 0.25 0.24 0.24 0.23 0.22 0.20 0.20
12=> 0.26 0.45 0.56 0.62 0.70 0.79 0.87 0.90
13=> 106.40 143.17 169.42 200.27 249.09 282.92 320.35 349.93
14=> 8.37 11.62 12.66 13.84 15.07 16.71 18.46 19.38
15=> 5.28 5.06 4.82 4.67 4.57 4.44 4.31 4.21
16=> 6.32 6.71 7.02 7.27 7.57 8.12 8.35 8.60
17=> 0.37 0.48 0.53 0.57 0.63 0.68 0.73 0.76
18=> 1.75 1.94 2.11 2.25 2.38 2.52 2.63 2.75
19=> 6.99 7.49 7.80 8.15 8.47 8.73 8.92 9.16
20=> 0.32 0.36 0.40 0.45 0.49 0.55 0.60 0.63
21=> 0.43 0.50 0.56 0.61 0.68 0.74 0.79 0.83
Результаты анализа информативности полной совокупности из 15 возможных комбинаций параметров представлены в таблице 1.
Таблица 1
Результаты анализа информативности спортивных параметров
|
№ ком- бина- ции |
Число параметров в комбинации |
Сочетания из номеров(1..4) и (/) из (1..21) |
СКО прогноза, см (**) |
Возможность прогноза до 14/17 лет (*) |
Название параметра |
Приме- чание |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1 |
1 |
(1)/(5) |
3.8 |
+/- |
возраст |
|
|
2 |
1 |
(2)/(14) |
3.1 |
+/+ |
СВТ |
мин |
|
3 |
1 |
(3)/(7) |
4.1 |
+/- |
Вес |
|
|
4 |
1 |
(4)/(2) |
4.6 |
+/- |
Рост |
макс |
|
5 |
2 |
(1,2)/(5,14) |
1.6 |
+/- |
||
|
6 |
2 |
(1,3)/(5,7) |
3.9 |
+/- |
||
|
7 |
2 |
(1,4)/(5,2) |
0.23 |
+/- |
мин |
|
|
8 |
2 |
(2,3)/(14,7) |
1.9 |
+/- |
||
|
9 |
2 |
(2,4)/(14,2) |
1.7 |
+/- |
||
|
10 |
2 |
(3,4)/(7,2) |
3.7 |
+ /- |
макс |
|
|
11 |
3 |
(1,2,3)/(5,14,7) |
0.7 |
+/- |
||
|
12 |
3 |
(1,2,4)/(5,14,2) |
0.2 |
+/- |
||
|
13 |
3 |
(1,3,4)/(5,7,2) |
0.1 |
+/- |
мин |
|
|
14 15 |
3 4 |
(2,3,4)/(14,7,2) (1,2,3,4)/(5,14,7,2) |
1.8 1.1 |
+/- +/- |
макс |
1->5 (x5) - возраст; 2->14 (x14)- степень использования силовых возможностей при отталкивании; 3->7 (x17) - вес; 4->2 (x2) - рост; (1,2,3,4)->(5,14,7,2).
(*) - прогноз проводится с малыми ошибками (+), с большими ошибками (-); (**) - СКО даны в период 10-14 лет; мин - минимум; макс - максимум.
Ниже приводятся графики оперативных динамических характеристик результативности (ОДХР).
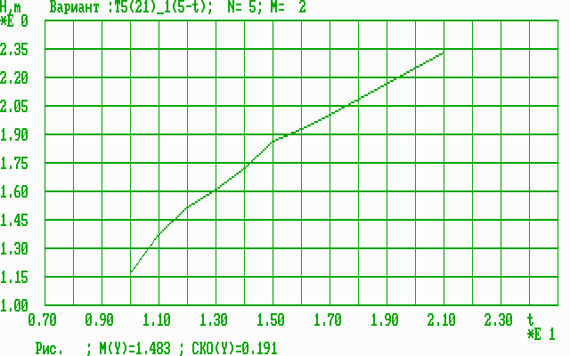
Рис. 1. Исходные данные средней результативности по годам.
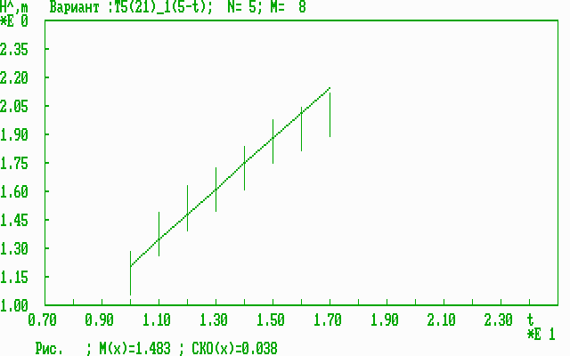
Рис. 2. Оперативная динамическая характеристика результативности для одномерного параметра (возраст).
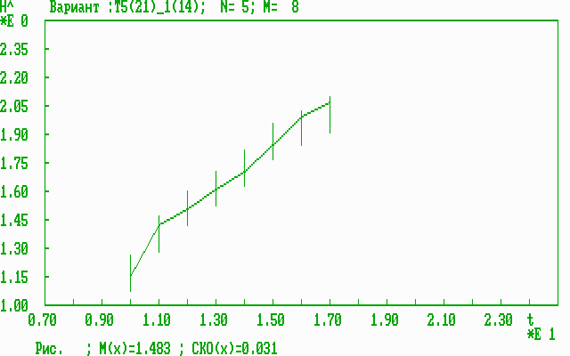
Рис. 3. Оперативная динамическая характеристика результативности для одномерного параметра (СВТ) - степени использования силовых возможностей при отталкивании.
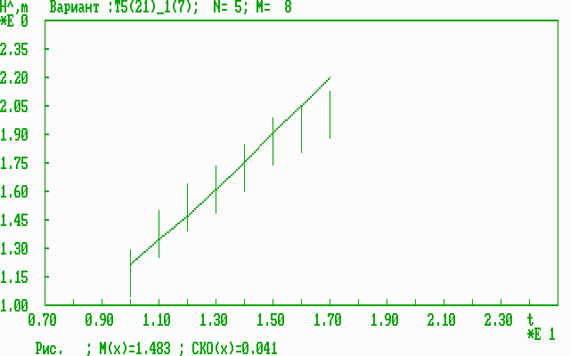
Рис. 4. Оперативная динамическая характеристика результативности для одномерного параметра (вес спортсмена).
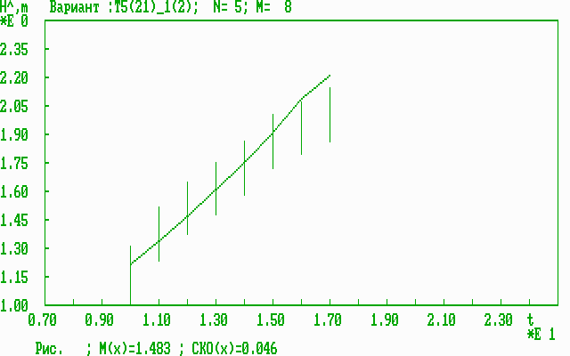
Рис. 5. Оперативная динамическая характеристика результативности для одномерного параметра (рост спортсмена).
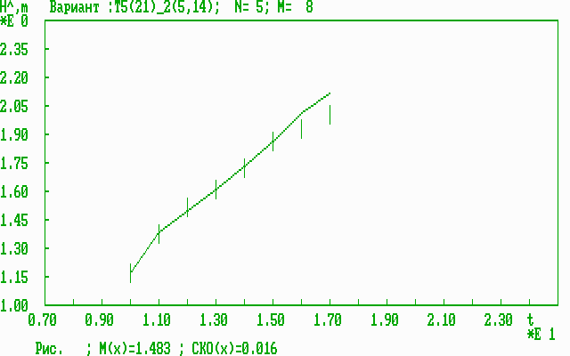
Рис. 6. Оперативная динамическая характеристика результативности для двумерного параметра (возраст, СВТ).
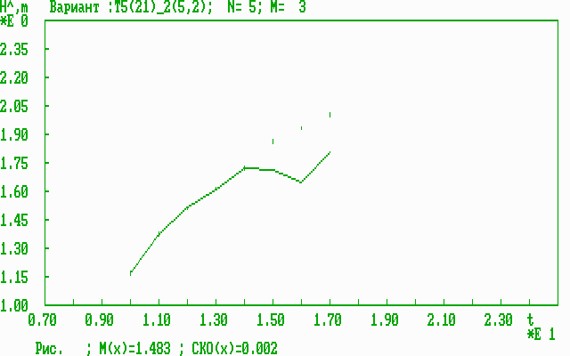
Рис. 7. Оперативная динамическая характеристика результативности для двумерного параметра (возраст, СВТ).
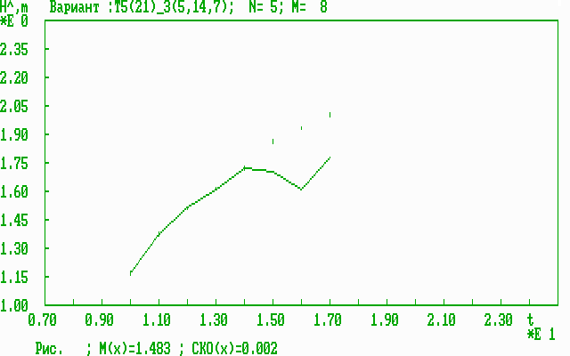
Рис. 8. Оперативная динамическая характеристика результативности для трехмерного параметра (возраст, СВТ, вес).
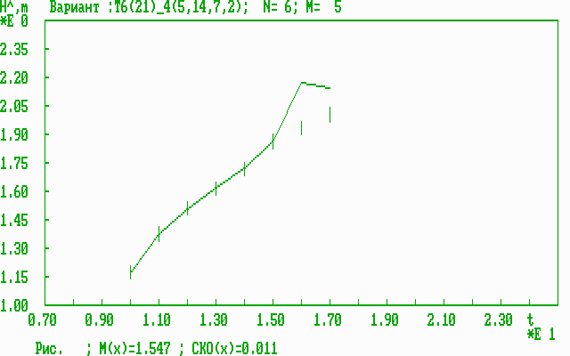
Рис. 9. Оперативная динамическая характеристика результативности для четырехмерного параметра (возраст, СВТ, вес, рост).
Выводы
Полученные экспериментальные результаты полностью подтверждают основные теоретические положения по решению задач прогноза результативности прыгунов в высоту. Среди рассмотренных одномерных параметров (СВТ, возраст, вес, рост) наиболее информативным параметром по прежнему [3] является СВТ, который в отличие от всех других параметров (одномерных, двумерных, трехмерных и четырехмерного) позволяет спрогнозировать результативность вплоть до 17 лет с СКО=3,1 см. Среди антропометрических параметров (вес, рост) более информативным оказывается вес (СКО=4,1 см). Среди двумерных параметров наиболее информативной комбинацией оказывается (возраст, рост) (СКО=0,23 см, однако только для периода 10-14 лет). Среди трехмерных параметров наиболее информативной комбинацией оказывается (возраст, вес, рост) (СКО=0,1 см, однако также для ограниченного периода 10-14 лет). Четырехмерный параметр (возраст, СВТ, вес, рост) уступает по информативности всем четырем трехмерным параметрам, что подтверждает теоретический вывод о том, что включение возраста в многомерные информативные параметры нецелесообразно, ввиду ограниченной точности численного решения задач прогноза и квазилинейной зависимости физических параметров от времени (возраста).
Дальнейшие исследования предполагается направить на изучение других проблем информативности степени использования силовых возможностей при отталкивании в сочетании с возрастом, весом и ростом прыгунов в высоту в задачах прогноза их результативности.
Литература
1. Ахметов Р.Ф. Групповые статистические характеристики и факторный анализ многомерной совокупности параметров спортсменов в задачах прогноза результативности // Педагогiка, психологiя та медико-бiологiчнi проблеми фiзичного виховання i спорту. - 2004. - № 6. - С. 91-104.
2. Ахметов Р.Ф. Прогноз результативности спортсменов на базе статистического факторного анализа и экспертного ранжирования полной совокупности антропометрических, технических и специализированных параметров // Педагогiка, психологiя та медико-бiологiчнi проблеми фiзичного виховання i спорту. - 2004. - № 7. - С. 82-95.
3. Ахметов Р.Ф. Анализ информативности степени использования силовых возможностей при отталкивании в задачах прогноза результативности прыгунов в высоту // Педагогiка, психологiя та медико-бiологiчнi проблеми фiзичного виховання i спорту. - 2004. - № 9. - С. 48-61.
4. Ахметов Р.Ф. Повышение точности раннего прогноза результативности спортсменов на базе расширения и динамической интерполяции их информативных физических параметров // Педагогiка, психологiя та медико-бiологiчнi проблеми фiзичного виховання i спорту. - 2004. - № 8. - С. 48-64.
5. Ахметов Р.Ф. До питання прогнозування результативностi стрибунiв у висоту // Науковий вiсник Волинського державного унiверситету iменi Лесi Украiнки. - 2004. - № 4. - С. 249-254.
Поступила в редакцию 28.05.2004г.