ОЦЕНКА ЭФФЕКТИВНОСТИ ТРЕНИРОВОЧНЫХ ПРОЦЕССОВ НА БАЗЕ ПОСЛЕДОВАТЕЛЬНОГО РЕШЕНИЯ ЗАДАЧ ПРОГНОЗА РЕЗУЛЬТАТИВНОСТИ СПОРТСМЕНОВ
Ахметов Р.Ф.
Житомирский государственный университет имени Ивана Франко
Аннотация. В статье рассматривается постановка задачи определения эффективности тренировочных процессов двух групп спортсменов в возрастные периоды 10-17 лет с позиций оценки минимального времени (возраста) достижения спортсменами рекордных результатов.
Ключевые слова: аппроксимация, регрессионная матрица, линейная регрессия.
Анотацiя. Ахметов Р.Ф. Оцiнка ефективностi тренувальних процесiв на базi послiдовного рiшення задач прогнозу результативностi спортсменiв. В статтi розглядаеться постановка задачi визначення ефективностi тренувальних процесiв двох груп спортсменiв у вiковi перiоди 10-17 рокiв з позицiй оцiнки мiнiмального часу (вiку) досягнення спортсменами рекордних результатiв.
Ключовi слова: апроксимацiя, регресiйна матриця, лiнiйна регресiя.
Annotation. Akhmetow R.F. Training Efficiency Criterion Based on the Consistent Analysis of Athlets’ Performance Prediction. The item addresses the problem of training efficiency criterion for two groups of athlets aged 10 through 17 based upon the evaluation of minimal time-consumption for achieving record-breaking results.
Key words: approximation, regression matrix, linear regression.
Постановка проблемы. Разработка методов количественной оценки эффективности тренировочного процесса является одной из важнейших задач теории и практики современного спорта. В последние годы украинским прыгунам в высоту не удается побеждать на крупных международных соревнованиях. Этот факт стимулирует специалистов продолжать разработку точности прогноза результативности прыгунов в высоту, что в значительной мере будет способствовать качественному отбору в этом виде спорта, а также количественной оценке эффективности тренировочного процесса.
Анализ последних исследований и публикаций. Прогнозирование - разработка прогнозов в спорте - является формой конкретизации предвидения перспектив развития того или иного процесса или явления, характерного для спортивной деятельности [5]. Прогнозирование тесно связано с управлением, потому что обеспечивает достаточно обоснованные предпосылки для принятия управленческих решений в сфере спортивной подготовки [6].
Работа продолжает цикл статей автора [1-4] по вопросам использования факторного анализа спортивных параметров и прогноза результативности спортсменов в связи с определением эффективности тренировочного процесса.
Исследования проводились по теме 1.4.7 "Совершенствование технического мастерства легкоатлетов-прыгунов в процессе многолетней подготовки" в соответствии с планом НИР Государственного комитета по физической культуре и спорту Украины на 2001-2005 гг. Номер госрегистрации: 0101U006316.
Целью настоящего исследования было оценить эффективность двух тренировочных процессов (по общепринятой и усовершенствованной методике) для двух групп спортсменов из 12 человек в возрастные периоды 10-17 лет.
Результаты исследования.
Средняя результативность группы спортсменов зависит, вообще говоря, нелинейным образом от средних физических параметров спортсменов
![]() , которые в свою очередь являются также нелинейными функциями времени
t (возраста) [2]:
, которые в свою очередь являются также нелинейными функциями времени
t (возраста) [2]:
![]() , (1)
, (1)
где Р - число информативных физических параметров спортсменов (в данной работе Р<15). Зависимость (1) называется далее оперативной динамической характеристикой результативности (ОДХР) [4]. Она неявным образом зависит от структуры тренировочного процесса (алгоритма тренировки или методики тренировки) и конкретного набора информативных физических параметров спортсменов:
![]() , (2)
, (2)
где ![]() - условное обозначение параметров тренировочного процесса для n-той методики подготовки спортсменов. Проведенный в данной работе анализ большого числа разнообразных ОДХР показывает, что её можно подразделить на интервале времени
- условное обозначение параметров тренировочного процесса для n-той методики подготовки спортсменов. Проведенный в данной работе анализ большого числа разнообразных ОДХР показывает, что её можно подразделить на интервале времени
![]() на три характерных участка (рис.
1): Т1=(a,t1), T2=(t1,t2), T3=(t2,b), где Т1 -
начальный нелинейный участок подросткового возраста (a<10 лет, t1<12 лет), Т2 -
средний квазилинейный участок (t2<18 лет), Т3 -
заключительный нелинейный участок (b> 18 лет),
на три характерных участка (рис.
1): Т1=(a,t1), T2=(t1,t2), T3=(t2,b), где Т1 -
начальный нелинейный участок подросткового возраста (a<10 лет, t1<12 лет), Т2 -
средний квазилинейный участок (t2<18 лет), Т3 -
заключительный нелинейный участок (b> 18 лет),
![]() - некоторый предельный результат для данного тренировочного процесса
- некоторый предельный результат для данного тренировочного процесса
![]() (например, для
"перекидного" способа
(например, для
"перекидного" способа ![]() ),
), ![]() -
рекордный результат (на сегодня в перспективе
-
рекордный результат (на сегодня в перспективе
![]() для способа "фосбери-флоп"),
для способа "фосбери-флоп"), ![]() -
потенциальный минимальный период достижения предельного результата
-
потенциальный минимальный период достижения предельного результата
![]() ,
, ![]() -
потенциальный минимальный период достижения рекордного результата
-
потенциальный минимальный период достижения рекордного результата
![]() .
.
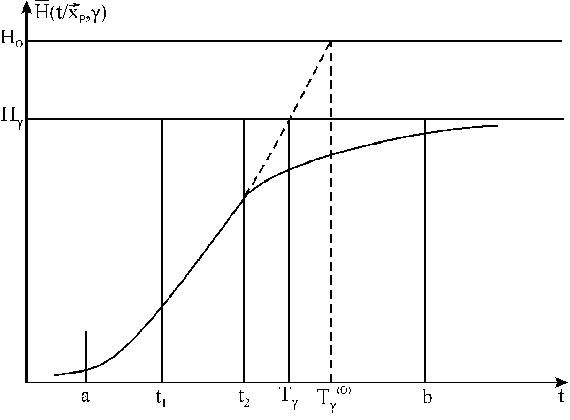
Рис. 1. Общий вид оперативной динамической характеристики результативности (ОДХР)
При этом ОДРХ на начальном и заключительном участках носит нелинейный характер, а на среднем участке - квазилинейный характер. Числовыми показателями эффективности того или иного тренировочного процесса являются следующие величины:
![]() . (3)
. (3)
Чем ближе предельный "алгоритмический" результат
![]() к рекордному результату
к рекордному результату
![]() и чем меньше периоды
и чем меньше периоды
![]() , тем более эффективен тренировочный процесс
, тем более эффективен тренировочный процесс
![]() . В данной работе основное внимание
уделяется среднему участку ОДХР (t1,t2) и показателю эффективности
. В данной работе основное внимание
уделяется среднему участку ОДХР (t1,t2) и показателю эффективности
![]() - потенциальному минимальному времени (возрасту) достижения рекордного результата (250 см). Отметим, что выделение именно линейной формы ОДХР на среднем участке подготовки спортсменов является априорно неопределенным и далеко нетривиальным решением. Заключение о допустимости квазилинейного характера ОДХР на среднем участке было сделано в данной работе в ходе экспериментального исследования большого числа ОДХР и решения соответствующих задач прогноза результативности спортсменов для различных групп спортсменов, для различных совокупностей информативных спортивных параметров и для различных тренировочных процессов. Существенно также отметить, что в данной работе ОДХР рассматривается с самого начала как функция
многих переменных (физических параметров
- потенциальному минимальному времени (возрасту) достижения рекордного результата (250 см). Отметим, что выделение именно линейной формы ОДХР на среднем участке подготовки спортсменов является априорно неопределенным и далеко нетривиальным решением. Заключение о допустимости квазилинейного характера ОДХР на среднем участке было сделано в данной работе в ходе экспериментального исследования большого числа ОДХР и решения соответствующих задач прогноза результативности спортсменов для различных групп спортсменов, для различных совокупностей информативных спортивных параметров и для различных тренировочных процессов. Существенно также отметить, что в данной работе ОДХР рассматривается с самого начала как функция
многих переменных (физических параметров
![]() ), а не как простая одномерная функция времени t. Сначала в результате решения статистической задачи линейной регрессии результативности на среднем участке ОДРХ оценивается линейная аппроксимация ОДХР [1]:
), а не как простая одномерная функция времени t. Сначала в результате решения статистической задачи линейной регрессии результативности на среднем участке ОДРХ оценивается линейная аппроксимация ОДХР [1]:
![]() (4)
(4)
и только затем оценивается одномерная зависимость ОДРХ (1) от времени t При этом точность линейной аппроксимации ОДХР растет с увеличением числа Р информативных спортивных параметров и оказывается значительно выше, чем точность простой одномерной линейной аппроксимации ОДХР [4]:
![]() ,
, ![]() . (5)
. (5)
Оценка максимальной скорости роста результативности и потенциального минимального времени достижения рекордных результатов
Согласно определению (3) для оценки эффективности тренировочного процесса достаточно оценить максимальную скорость роста результативности на линейном участке ОДХР:
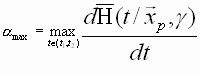 . (6)
. (6)
Если решена задача прогноза (линейной регрессии) результативности по наблюдениям вектора физических параметров
![]() на интервале времени
на интервале времени
![]() , то можно сделать соответствующую линейную аппроксимацию ОДХР и оценить максимальную скорость роста результативности:
, то можно сделать соответствующую линейную аппроксимацию ОДХР и оценить максимальную скорость роста результативности:
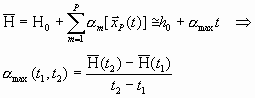 (7)
(7)
Тогда оценка потенциального минимального времени достижения рекордного результата представляется в виде:
![]() . (8)
. (8)
Адаптация тренировочного процесса в ходе последовательного решения задач прогноза результативности на линейном участке ОДРХ
Для построения полной ОДХР для некоторого тренировочного процесса требуется, вообще говоря, хотя бы один "полный" цикл тренировочного процесса отдельно взятой группы (например, в возрастах 10-17 лет) или некоторого множества групп с тем же тренировочным процессом. Однако, для каждой новой группы спортсменов можно и целесообразно анализировать текущую скорость роста результативности:
![]()
и она не обязательно будет монотонно-возрастающей функцией времени. В случае, если для некоторого моментов времени
![]() оказывается нарушение монотонности:
оказывается нарушение монотонности:
![]() , (9)
, (9)
то в этом случае требуется проанализировать исходную многомерную зависимость ОДХР (4) от множества физических параметров
![]() и принять меры по обеспечению более высоких показателей того или иного наиболее информативного и значимого физического спортивного параметра (например, увеличить на 5% степень использования силовых возможностей при отталкивании). Таким образом можно обеспечить адаптацию тренировочного процесса в ходе последовательного во времени решения задач прогноза результативности группы спортсменов на линейном участке ОДХР.
и принять меры по обеспечению более высоких показателей того или иного наиболее информативного и значимого физического спортивного параметра (например, увеличить на 5% степень использования силовых возможностей при отталкивании). Таким образом можно обеспечить адаптацию тренировочного процесса в ходе последовательного во времени решения задач прогноза результативности группы спортсменов на линейном участке ОДХР.
Результаты оценки эффективности двух тренировочных процессов
В данном разделе на основании проведенных ранее теоретических исследований по факторному анализу спортивных параметров [1] , прогнозу результативности спортсменов [2-4] и критериям эффективности тренировочных процессов проводится экспериментальное исследование на примере 2-х групп в динамике 10-17 лет с различными тренировочными процессами (общепринятым и усовершенствованным). Расширенный перечень [1] антропометрических, технических и специализированных параметров спортсменов сокращен для простоты с 21-го до 15 параметров:
РАСШИРЕННЫЙ ПЕРЕЧЕНЬ из 15 ПАРАМЕТРОВ СПОРТСМЕНОВ
- Спортивный результат ( Целевая функция)
- Рост.
- Вес.
- Скорость разбега перед отталкиванием.
- Скорость вылета ОЦТ (в момент отрыва).
- Угол вылета ОЦТ.
- Длительность фазы отталкивания.
- Высота вылета ОЦТ.
- Степень использования силовых возможностей толчка (%).
- Бег - 30 м. (с).
- Скорость спринтерского бега ( 10 м. с хода).
- Прыжок вверх с двух ног с места.
- Прыжок в длину с места.
- Прыжок вверх с толчковой ноги (махом другой).
- Прыжок вверх с трех шагов разбега.
АНТРОПОМЕТРИЧЕСКИЕ ПАРАМЕТРЫ (2-3)
ТЕХНИЧЕСКИЕ ПАРАМЕТРЫ (4-9)
(Регистрируемые и расчетные показатели техподготовки)
СПЕЦИАЛИЗИРОВАННЫЕ ПАРАМЕТРЫ (10-15)
(Уровень спецфизподготовки)
Ранжирование по Саати [2] 14 указанных параметров представлено в таблице 1.
Таблица 1.
Ранжировка 20 параметров по Саати (номера из 1-21 и из 1-15 )
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
12 |
14 |
9 |
13 |
21 |
8 |
15 |
16 |
11 |
10 |
20 |
2 |
17 |
18 |
19 |
7 |
3 |
4 |
5 |
6 |
|
8 |
9 |
5 |
15 |
4 |
10 |
11 |
7 |
6 |
14 |
2 |
12 |
13 |
(2 строка - номер параметра из 1-21; 3 строка - номер параметра из 1-15)
Статистические характеристики спортивных параметров для 2-х групп были рассчитаны программой факторного анализа fakPS [1]. Затем была использована программа регрессионного анализа и прогноза результативности спортсменов corr2din [2-4] для получения и анализа оперативных динамических характеристик результативности (ОДХР), (рисунки 2, 3) и сравнения эффективности рассматриваемых тренировочных процессов.
Результаты регрессионного анализа ОДХР и сравнительный анализ эффективности тренировочных процессов
А. Группа-0 (экспериментальная с усовершенствованным тренировочным процессом)
Программа РЕГРЕССИЯ_1д (cor2din)
Статистические ПАРАМЕТРЫ МОДЕЛИ ПРОГНОЗА:
Имя файла данных: g015_9.dat
Число параметров Nmax=15
Число возрастных групп (включая мастеров) Mmax= 9
Возрастная группа 0
Исх. данные по 15 параметрам и 9-ти годам (9-мастера)
1=> 131.25 148.08 162.67 175.08 186.92 197.50 204.25 209.92 233.00
2=> 150.67 154.00 158.83 163.17 169.67 174.75 180.75 186.42 193.00
3=> 36.17 39.67 43.08 47.08 51.17 57.58 63.25 68.42 75.08
4=> 4.79 5.15 5.53 5.84 6.02 6.34 6.74 7.15 7.67
5=> 3.43 3.67 3.98 4.22 4.44 4.83 5.18 5.47 5.17
6=> 51.42 51.74 52.06 52.35 52.59 53.19 53.98 54.88 56.96
7=> 258.33 236.67 224.17 212.50 205.83 196.67 185.00 171.67 140.00
8=> 46.58 55.58 65.50 71.33 77.08 82.58 88.33 92.58 107.00
9=> 11.82 13.64 15.01 16.48 18.05 19.61 21.14 22.95 40.37
10=> 5.05 4.83 4.61 4.41 4.27 4.13 4.00 3.88 3.84
11=> 6.92 7.24 7.54 7.81 8.07 8.32 8.63 8.95 10.34
12=> 40.50 45.58 51.08 57.08 64.17 70.83 77.50 83.50 91.00
13=> 188.17 200.83 212.25 222.83 233.92 251.08 266.75 283.50 315.00
14=> 34.50 40.67 48.08 53.42 58.50 63.67 68.25 72.25 87.00
15=> 43.83 52.50 62.00 67.83 74.00 79.92 86.08 90.25 109.00
Программа RegRNm-din
Шифр цепи: T5o(15)_3(8,5,15)
Объем выборки по годам (или полугодам),Nmin=3 ( N>M), N= 5
начальный(a) и конечный(b) возрасты для прогноза10.00 14.00
Размерность вектора параметров регрессии, вкл. Н0), N>M>1, Mmin=2; M= 4
Число параметров из 15, k=m-1=3
Bектор номеров информативных параметров VN(2-15)
2=>8
3=>5
4=>15
Нормированная корреляционная матрица оценок вектора регрессии
1=> 1.0000 -0.7635 -0.9957 0.8636
2=> -0.7635 1.0000 0.7104 -0.9846
3=> -0.9957 0.7104 1.0000 -0.8222
4=> 0.8636 -0.9846 -0.8222 1.0000
Решение системы уравнений регрессии
Средние коэффициенты регрессии:
I[1]= 59.390279
I[2]= -2.710007
I[3]= -1.011768
I[4]= 4.609529
Оценка вектора Y^ по регрессии
Y^[1]= 131.72611 Y=>131.250000
Y^[2]= 147.04199 Y=>148.083000
Y^[3]= 163.64575 Y=>162.667000
Y^[4]= 174.48082 Y=>175.083000
Y^[5]= 187.10569 Y=>186.917000
Несмещенная оценка дисперсии s*s=2.666569; s=1.632963
СКО оценок параметров регрессии
1=> 89.478
2=> 4.608
3=> 42.502
4=> 5.791
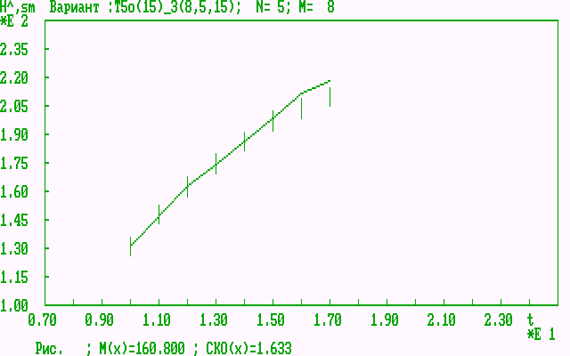
Рис. 2. Оперативная динамическая характеристика результативности для экспериментальной группы с усовершенствованным тренировочным процессом
Показатель эффективности тренировочного процесса: ![]() лет.
лет.
Б. Группа-1 (контрольная группа с общепринятым тренировочным процессом)
Программа РЕГРЕССИЯ_1д (cor2din)
Статистические ПАРАМЕТРЫ МОДЕЛИ ПРОГНОЗА:
Имя файла данных: g115_9.dat
Число параметров Nmax=15
Число возрастных групп (включая мастеров) Mmax= 9
Возрастная группа 1
Исх. данные по 15 параметрам и 9-ти годам (9-мастера)
1=> 125.83 136.58 153.08 165.08 174.58 185.00 192.58 198.00 233.00
2=> 149.67 153.83 158.08 162.42 168.75 173.25 178.08 184.17 193.00
3=> 39.00 43.67 48.75 52.92 59.33 64.42 69.75 76.83 75.08
4=> 4.57 4.77 4.98 5.22 5.39 5.59 5.87 6.22 7.67
5=> 3.25 3.44 3.63 3.88 4.08 4.30 4.67 4.82 5.17
6=> 49.12 50.15 50.75 51.29 51.84 52.24 52.67 53.07 56.96
7=> 271.67 255.00 244.17 234.17 229.17 220.00 210.00 201.67 140.00
8=> 41.00 47.58 56.08 62.25 67.08 72.50 77.50 82.25 107.00
9=> 7.94 9.52 11.36 12.71 14.27 15.68 17.23 18.52 40.37
10=> 5.26 5.03 4.88 4.70 4.55 4.41 4.29 4.17 3.84
11=> 6.63 6.72 6.88 7.22 7.52 7.68 7.97 8.22 10.34
12=> 39.83 38.33 45.75 48.83 55.92 61.67 69.67 74.67 91.00
13=> 187.75 198.50 207.83 220.83 230.75 248.25 263.83 278.58 315.00
14=> 28.83 32.92 39.75 45.17 50.67 53.92 59.42 64.25 87.00
15=> 38.08 44.58 53.25 58.50 63.92 69.58 74.75 79.83 109.00
Программа RegRNm-din
Шифр цепи: T5e(15)_3(8,5,15)
Объем выборки по годам (или полугодам),Nmin=3 ( N>M), N= 5
начальный(a) и конечный(b) возрасты для прогноза10.00 14.00
Размерность вектора параметров регрессии, вкл. Н0), N>M>1, Mmin=2; M= 4
Bектор номеров информативных параметров VN(2-15)
Число параметров из 15, k=m-1=3
2=>8
3=>5
4=>15
Нормированная корреляционная матрица оценок вектора регрессии
1=> 1.0000 0.2795 -0.9813 -0.0868
2=> 0.2795 1.0000 -0.4285 -0.9795
3=> -0.9813 -0.4285 1.0000 0.2395
4=> -0.0868 -0.9795 0.2395 1.0000
Нормированная корреляционная матрица входных данных
1.000 0.999 0.993 0.999
0.999 1.000 0.991 1.000
0.993 0.991 1.000 0.990
0.999 1.000 0.990 1.000
Решение системы уравнений регрессии
Средние коэффициенты регрессии:
I[1]= 31.486257
I[2]= 1.565326
I[3]= 8.416482
I[4]= 0.057864
Оценка вектора Y^ по регрессии
Y^[1]= 125.22180 Y=>125.833000
Y^[2]= 137.51842 Y=>136.583000
Y^[3]= 152.86540 Y=>153.083000
Y^[4]= 164.99400 Y=>165.083000
Y^[5]= 174.55597 Y=>174.583000
Несмещенная оценка дисперсии s*s=1.304569; s=1.142177
СКО оценок параметров регрессии
1=> 25.608
2=> 2.030
3=> 13.392
4=> 1.925
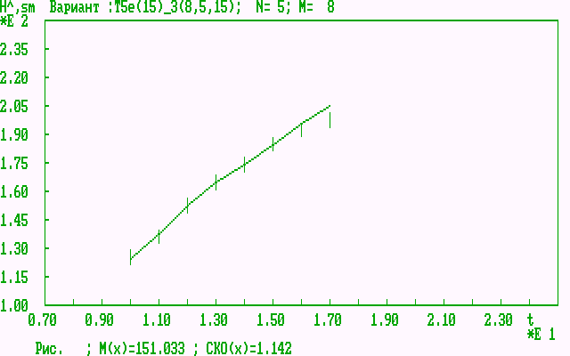
Рис. 3. Оперативная динамическая характеристика результативности для контрольной группы с общепринятым тренировочным процессом
Показатель
эффективности тренировочного процесса: ![]() год.
год.
Анализ ОДХР для рассмотренных выше тренировочных процессов показывает, что усовершенствованный тренировочный процесс выигрывает по результативности в среднем 10 см, а по эффективности - 2 года.
Выводы: 1. Важнейшей характеристикой тренировочного процесса является т.н. оперативная динамическая характеристика результативности (ОДХР) в виде зависимости от времени средней результативности (в группе), как функции многих переменных - физических спортивных параметров. ОДХР можно подразделить на три характерных участка: начальный - нелинейный, средний - квазилинейный и заключительный - нелинейный.
2. Достаточно информативным показателем эффективности тренировочного процесса является потенциальное минимальное время достижения рекордного результата. Оно обратно пропорционально максимальной скорости роста результативности на линейном участке ОДХР.
3. Оптимизацию тренировочного процесса целесообразно проводить путем последовательного решения задач прогноза результативности для различного числа информативных спортивных параметров для последовательных текущих временных интервалов (возрастных периодов 12-17 лет).
4. Адаптация тренировочного процесса при наличии снижения текущей скорости роста результативности заключается в анализе регрессионной формулы для результативности, как линейной функции многих физических параметров и принятии решения об обеспечении повышения показателей наиболее информативных и значимых спортивных параметров.
5. Анализ ОДХР для рассмотренных выше тренировочных процессов показывает, что разработанный тренировочный процесс выигрывает по результативности в среднем 10 см, а по эффективности - 2 года.
Дальнейшие исследования предполагается провести в направлении изучения других проблем оценки эффективности тренировочных процессов на базе последовательного решения задач прогноза результативности спортсменов.
Литература
1. Ахметов Р.Ф. Групповые статистические характеристики и факторный анализ многомерной совокупности параметров спортсменов в задачах прогноза результативности // Педагогiка, психологiя та медико-бiологiчнi проблеми фiзичного виховання i спорту. - 2004. - № 6. - С. 91-104.
2. Ахметов Р.Ф. Прогноз результативности спортсменов на базе статистического факторного анализа и экспертного ранжирования полной совокупности антропометрических, технических и специализированных параметров // Педагогiка, психологiя та медико-бiологiчнi проблеми фiзичного виховання i спорту. - 2004. - № 7. - С. 82-95.
3. Ахметов Р.Ф. Анализ информативности степени использования силовых возможностей при отталкивании в задачах прогноза результативности прыгунов в высоту // Педагогiка, психологiя та медико-бiологiчнi проблеми фiзичного виховання i спорту. - 2004. - № 9. - С. 48-61.
4. Повышение точности раннего прогноза результативности спортсменов на базе расширения и динамической интерполяции их информативных физических параметров // Педагогiка, психологiя та медико-бiологiчнi проблеми фiзичного виховання i спорту. - 2004. - № 7. - С. 48-64.
5. Платонов В.Н. Общая теория подготовки спортсменов в олимпийском спорте. - К.: Олимпийская литература, 1997. - 583 с.
6. Плахтиенко В.А., Мельник В.Г. Прогнозирование в спорте. - Л.: ВДКИФК, 1980. - 79 с.
Поступила в редакцию 23.04.2004г.